雙紐線

雙紐線是數學的一種術語。雙紐線也稱伯努利雙紐線，設定線段AB長度為2a,動點M滿足MA*MB=a^2那么M的軌跡稱為雙紐線。

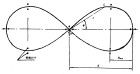
方程

取AB為x軸，中點為原點，那么A,B坐標分別為(-a,0),(a,0)

設M(x,y),則

根號[(x+a)^2+y^2]*根號[(x-a)^2+y^2]=a^2

整理得

(x^2+y^2)^2=2a^2(x^2-y^2)

這就是 雙紐線直角坐標方程。

在Mathematica中繪製雙紐線的語句為：

PolarPlot[{Sqrt[2 Cos[2 t]], -Sqrt[2 Cos[2 t]]}, {t, 0, Pi}]

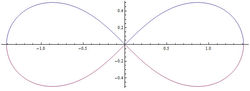雙紐線

圖形如右圖：

在極坐標中，可化簡得

ρ^2=2a^2*cos2θ

另一個雙紐線的方程是：ρ^2=2a^2*sin2θ

極坐標方程下：x=ρcosθ,y=ρsinθ

ρ^2=2a^2*cos2θ的導數方程：ρ=-sin(2θ)*(a^2×cos2θ)^(-0.5)

ρ^2=2a^2*sin2θ的導數方程：ρ=(sin(2θ)*a^2)^(-0.5)*cos(2θ)

雙紐線可通過等軸雙曲線經過反演得到