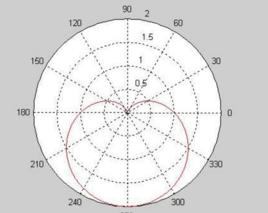
基本性質
a=1時的心臟線的周長為 8,圍得的面積為3π/2。
心臟線亦為蚶線的一種。
在 Mandelbrot set 正中間的圖形便是一個心臟線。
心臟線的英文名稱“Cardioid”是 de Castillon 在 1741年 的《Philosophical Transactions of the Royal Society》發表的;意為“像心臟的”。
數學表達
極坐標方程
水平方向: ρ=a(1-cosθ) 或 ρ=a(1+cosθ) (a>0)
垂直方向: ρ=a(1-sinθ) 或 ρ=a(1+sinθ) (a>0)
直角坐標方程
心形線的平面直角坐標系方程表達式分別為 x^2+y^2+a*x=a*sqrt(x^2+y^2) 和 x^2+y^2-a*x=a*sqrt(x^2+y^2)
參數方程
x=a*(2*cos(t)-cos(2*t))y=a*(2*sin(t)-sin(2*t))
所圍面積為3/2*PI*a^2,形成的弧長為8a。
心臟線的歷史
Christine是十七世紀時瑞典的一位公主,她美麗善良,而且很聰明,尤其很喜歡數學。有一天她換上了便服去王宮外面,路上看到很多乞丐,其中有一個很特別,他不主動請求過路人施捨,而是安靜地蹲在地上專心研究數學問題。那個人並不知道站在他眼前的小姐就是公主,只是很驚訝於這位年輕小姐言談之間顯露出來的數學才華,便很高興地和Christine交談起來。Christine公主這才知道,他原本是一個數學家,可惜因為某些原因在法國做數學不得志,窮困落魄,最後流浪到瑞典來的。於是Christine公主把這個數學家請到王宮裡做她的數學老師,兩個人一起討論數學問題,一起談天說地,日久天長,兩個人就這樣沉浸在只屬於他們兩個人的數學世界和愛情世界裡,很幸福,很快樂。
但是Christine的父親知道了女兒戀愛的事。這個固執的國王根本不把數學和數學家放在眼裡,他覺得那個法國小子配不上自己的女兒,於是強硬地拆散他們,把數學家驅散出境,永遠不許他邁進自己的國家一步,還扣壓了之後他寫給公主的所有的信……愛人離開之後的杳無音訊,使Christine變得沉默寡言,不再喜歡和任何人說話……因為這個世界上可以和她溝通討論的只有那個人啊!
那個人回到法國後感染上了黑死病,即將死去。他在臨死前給他的公主,他的愛人,Christine,寄出了第十三封信,也是最後一封。這一次國王拆了信卻看不懂他寫的是什麼。交給大臣們去看,大臣們也看不懂。請了很多數學家來看,還是看不懂。最後國王沒辦法,只好把信交還給了Christine。
Christine打開她的愛人留給她的最後的信,發現上面只有一個簡單的數學式:r = a(1-sinθ)。
是的,別人看不懂這是什麼,可是她知道!那是他們以前一起討論過的二維坐標呀。用代數來表示平面的幾何坐標,這個從來沒有人研究過的數學問題,全世界只有那個人和Christine知道,這是他和她之間的秘密。
於是她找出紙和筆,按照數學式畫起圖來……這是一顆心的形狀,後來人們就把它叫做心臟線。他還愛著她!他直到死都還愛著她。她知道。全世界只有她知道。
一直以來,人們以為這位用心臟線傳情的人就是笛卡爾,然而,據考證,笛卡爾於1649年冬,笛卡爾應瑞典女王克里斯蒂安(也就是上文的Christine)的邀請,來到了斯德哥爾摩,任宮廷哲學家,為瑞典女王授課(女王已經登基,笛卡爾也並沒有遭到驅逐)。1650年初患肺炎抱病不起,同年二月病逝於瑞典(不是在法國死於黑死病)。由此可見,故事中的數學家並非笛卡爾,要么另有其人,要么,這個故事只是美麗的謊言。
如何畫心臟線
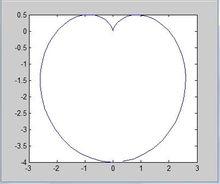 圖1
圖1示例:在MATLAB中,輸入下列指令,即可得到如圖1所示的心臟線:
i=-pi:0.1:pi;
x=2.*(sin(i)-sin(2*i)./2);
y=2.*(cos(i)-cos(i).^2);
plot(x,y)
此外,還可儀用逐點生成算法實現,詳見參考文獻 。