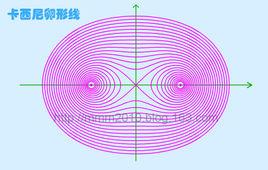
定義
卡西尼卵形線是由到兩個定點(叫做焦點)距離之積為常數的所有那些點組成的圖形。
 卡西尼卵形線
卡西尼卵形線圖形分支
設兩定點為A,B,AB=2c,動點M滿足MA*MB=a^2(a>0為定值)
當a<c時,圖象分為兩支,隨著a的減小而分別向A,C收縮。
當a=c時的分支,成8形自相交叉,稱為雙紐線
當c<a<c√2時,圖象是一條沒有自交點的光滑曲線,曲線中部有凹進的細腰。
當a=c√2時,與前種情況一樣,但曲線中部變平。
當a>c√2時,曲線中部凸起。
卡西尼卵形線圖象由此組成。
直角坐標方程
取AB為x軸,中點為原點,則
根號[(x+c)^2+y^2]*根號[(x-c)^2+y^2]=a^2
整理得(x^2+y^2)^2-2c^2(x^2-y^2)=a^2-c^4
當a=c時退化為雙紐線方程。
取兩個定點 Q1, Q2為焦點。 卡西尼卵形線(Cassini oval)是所有這樣的點P的軌跡: P和焦點的距離的積為常數(這類似橢圓的定義——點 P和焦點的距離的和為常數)。即。
在直角坐標系,若焦點分別在( a,0)和( − a,0),卵形線的方程可寫成:
(( x− a) + y)(( x+ a) + y) = b( x+ y) − 2 a( x− y) + a= b( x+ y+ a) − 4 a x= b在極坐標系:
r− 2 a rcos2θ = b− a卵形線經過反演變換,依然是卵形線。
卵形線的形狀由 b/ a的值決定。若 b/ a> 1,軌跡是一個封閉的圈。若 b/ a< 1,軌跡是兩個封閉的圈。若 b/ a= 1,軌跡為伯努利雙紐線。