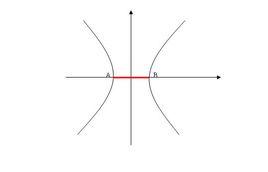
雙曲線與坐標軸兩交點的連線段AB叫做實軸 。實軸的長度為2a(a為標準方程中的參數)。
相關詞條
-
等軸雙曲線
實軸和虛軸相等的雙曲線叫作等軸雙曲線(直角雙曲線) 。 等軸雙曲線是指一種特殊的雙曲線,特點是漸近線互相垂直,半實軸長與半虛軸長相等,兩條漸近線y=±x...
主要性質 相關命題 -
實軸
實軸分為雙曲線中的實軸及複數平面中的實軸兩類。雙曲線中,雙曲線與坐標軸兩交點的連線段AB叫做實軸,長度為2a;複數域中,複數域與 x 軸上的點一一對應,...
雙曲線中的實軸 複數中的實軸 -
共軛雙曲線
共軛雙曲線是兩條具有特殊位置的雙曲線,如果一雙曲線的實軸及虛軸分別為另一雙曲線的虛軸及實軸,則此二雙曲線互為共軛雙曲線。它們有相同的漸近線,並且4個焦點...
定義 相關性質定理 例題解析 -
雙曲線漸近線
漸近線定義為如果曲線上的一點沿著趨於無窮遠時,該點與某條直線的距離趨於零,則稱此條直線為曲線的漸近線。雙曲線漸近線方程,是一種幾何圖形的算法,這種主要解...
基本公式 幾何性質 標準方程 注意事項 本節學習要求 -
雙曲線
一般的,雙曲線(希臘語“ὑπερβολή”,字面意思是“超過”或“超出”)是定義為平面交截直角圓錐面的兩半的一類圓錐曲線。它還可以定義為與兩個固定的點(...
名稱定義 特徵介紹 實際套用 光學性質 -
雙曲線準線
平面內到一個定點與一條定直線的距離之比是一個大於1的常數的動點的軌跡是雙曲線,這個常數即該雙曲線的離心率,定點是雙曲線的焦點,定直線是雙曲線的準線。
第一定義 方程 公式 -
等邊雙曲線
實軸和虛軸等長的雙曲線叫做等邊雙曲線。 此時,在雙曲線方程x^2/a^2-y^2/b^2=1中,a=b,於是得x^2-y^2=a^2。 雙曲線的漸近線方...
-
雙曲線漸近線方程
雙曲線漸近線方程,是一種幾何圖形的算法,這種主要解決實際中建築物在建築的時候的一些數據的處理。雙曲線的主要特點:無限接近,但不可以相交。分為鉛直漸近線、...
漸近線特點 幾何性質 注意 -
雙曲線的參數方程
雙曲線的參數方程是以焦點(c,0)和(-c,0)為圓心,R為變半徑的曲線方程。
定義 證明