雙曲線的參數方程

雙曲線的參數方程是以焦點（c，0）和（-c,0）為圓心，R為變半徑的曲線方程。

定義

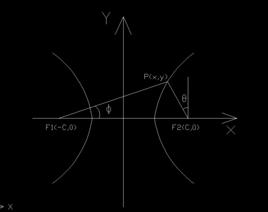
設雙曲線的兩個焦點分別為F1，F2，它們之間的距離為2c，雙曲線上任意一點到F1，F2的距離差為2a（a<c）。

以F1，F2所在直線為x軸，線段F1F2的垂直平分線為y軸，建立直角坐標系xOy，則F1,F2的坐標分別為（-c,0)，（c,0)。

參數方程為

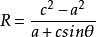雙曲線的參數方程

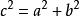雙曲線的參數方程

a為雙曲線實軸的一半，b為雙曲線虛軸的一半，c為焦距的一半；R為雙曲線上的點P(x，y)到焦點(c，0)的距離和雙曲線 上的點P(x，y)到焦點(-c，0)的距離，θ為雙曲線上點P(x，y)與焦點（c，0）的連線與y軸夾角，ф為雙曲線上點P（x,y)與焦點（-c,0)的連線與x軸夾角。

證明

推導得：

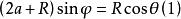雙曲線的參數方程

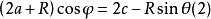雙曲線的參數方程

(1)的平方加(2)的平方

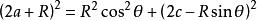雙曲線的參數方程

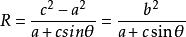雙曲線的參數方程

化簡得

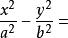雙曲線的參數方程

證明：將任意一點P的坐標（Rsinθ-c,Rcosθ)代入方程

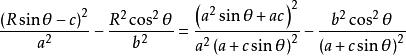雙曲線的參數方程

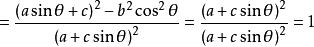雙曲線的參數方程

說明P點是雙曲線標準方程上的一點。