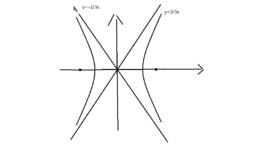
雙曲線中的實軸
雙曲線與坐標軸兩交點的連線段AB叫做實軸。實軸的長度為2a(a為標準方程中的參數)。
習慣稱X軸為實軸,y軸為虛軸。
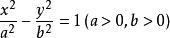 實軸
實軸在標準方程中,令y=0,得x=±a,即點A(-a,0)、A(a,0)為雙曲線與x軸的兩個交點,且A是左支上最右邊的點,A為右支上最左邊的點,這兩個點稱為雙曲線的頂點。
令x=0,y =-b ,無實數解但為便於作圖將點B(0,-b)、B(0,b)作在y軸上。
線段AA叫做雙曲線的實軸,長等於2a;BB叫做雙曲線的虛軸,長等於2b。
作出雙曲線的實虛軸可方便作出漸近線,繼而作出雙曲線的圖線。當實虛軸長相等時,這樣的雙曲線叫等軸雙曲線,且兩漸近線互相垂直。若以已知雙曲線的虛軸為實軸,實軸為虛軸的雙曲線叫做原雙曲線的共軛雙曲線,互為共軛雙曲線的兩雙曲線有共同的漸近線,四個交點在同一個圓上。
複數中的實軸
複數的幾何表示
[geometric representation of complex number]
複數可以用平面上的點表示。這使人們對複數有了真實感,同時使複數及複變函數在幾何與各種平面物理問題中有了廣泛的套用。
在平面上取定直角坐標系 xOy。這時平面上的點 P=(x,y) 便對應於複數 z=x+iy。所以,複數域與平面上的點建立了一一對應。顯然,全體實數與 x 軸上的點一一對應。因此,我們把 x 軸稱為實軸;而 y 軸稱為虛軸(imaginary axis)。與複數建立了這種關係的平面稱為複平面(complex plane),這時,平面也稱為高斯平面(Gaussian plane)。
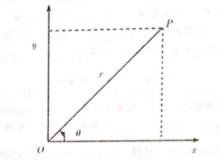 圖1
圖1 實軸
實軸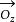 實軸
實軸如右圖所示,一個非零複數 z=x+iy 可看成是一個從原點出發到點 z 的向量 ,其長度就是複數 z 的模。該向量與 x 軸的正方向之間的夾角稱為複數 z 的幅角(argument),記作 Arg(z)。換句話說,複數的幅角就是 x 軸的正方向向量沿逆時針方向旋轉到向量 的位置所掃過的角度。但是,它是一個有向角,即它依賴於旋轉的方向,即沿逆時針旋轉是的幅角規定為正值;而沿順時針方向旋轉時,幅角規定為負值。
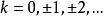 實軸
實軸顯然一個非零複數有無窮多個幅角。若θ 是非零複數 z 的任一給定的幅角,則 Arg(z)=θ+2kπ 都是 z 的幅角,其中 k=0, 。當我們對幅角取值範圍作某種規定後,比如要求幅角大於 -π 並小於或等於π ,這時一個非零複數的幅角就是唯一確定的。這種幅角的值稱為主值(princip value),記為 arg(z)。
顯然,有
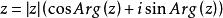 實軸
實軸此式稱為複數的三角函式表示式(trigonometric function representation of complex numbers)。
有了複數的幾何表示後,複數的運算也就有了幾何意義:兩複數相加就相當與兩個向量,按照平行四邊形法則相加:兩個複數相乘,其積點模等於它們的模的積,其積點幅角等於他們的幅角的和。