定義
雙曲正切函式（tanh）是雙曲正弦函式（sinh）與雙曲餘弦函式（cosh）的比值，其解析形式為 ：
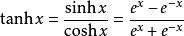雙曲正切函式
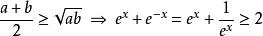雙曲正切函式
雙曲正切函式考慮不等關係：可知，雙曲正切函式的定義域為實數域。
運算
導數
雙曲的導數是雙曲餘弦的平方的倒數，即：
雙曲正切函式積分
雙曲正切函式的不定積分有如下形式 ：
雙曲正切函式
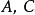雙曲正切函式式中為常數。
泰勒展開
雙曲正切函式的泰勒展開式為 ：
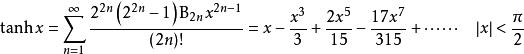雙曲正切函式
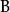雙曲正切函式式中為伯努力數（Bernoulli number）。
反函式
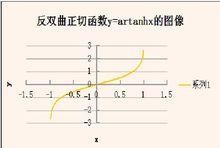反雙曲正切函式的圖像雙曲正切函式的反函式是反雙曲正切函式，其定義為 ：
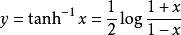雙曲正切函式函式的定義域為開區間（-1,1），它在開區間（-1,1）內是單調增加的奇函式，圖形關於原點對稱。
與其他雙曲函式的關係
除了雙曲正切函式的定義式外，雙曲正切函式還有以下式子。
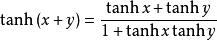雙曲正切函式1、和角公式：
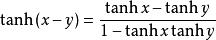雙曲正切函式2、差角公式：（和角公式的推導）
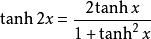雙曲正切函式3、二倍角公式：（和角公式的推導）
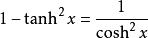雙曲正切函式4、恆等式：
性質
有界性
雙曲正切函式的圖形夾在水平直線y=1及y=-1之間，且當x的絕對值很大時，它的圖形在第一象限內接近於直線y=1，而在第三象限內接近於直線y=-1。
即雙曲正切函式的值域是(-1,1)。
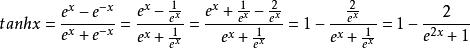雙曲正切函式證明：
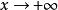雙曲正切函式
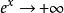雙曲正切函式
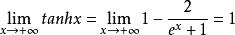雙曲正切函式當 時，由於 ,則 。
雙曲正切函式
雙曲正切函式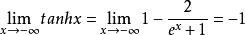
雙曲正切函式當 時，由於 ，則 。
奇偶性
雙曲正切函式是奇函式，它的圖形通過原點且關於原點對稱 。
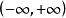雙曲正切函式下面是證明：首先明確雙曲正切函式的定義域是 。
雙曲正切函式。
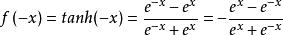雙曲正切函式而
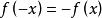雙曲正切函式得出，則證明出雙曲正切函式為奇函式。
周期性
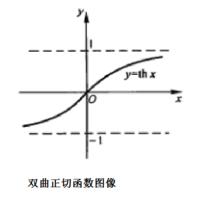雙曲正切函式的圖像無論是雙曲正切函式y=tanhx，還是雙曲正弦函式y=sinhx、雙曲餘弦函式y=coshx，它們都不是周期函式。
單調性
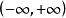雙曲正切函式雙曲正切函式在區間 內是單調增加的。
證明如下：
對雙曲正切函式求導。
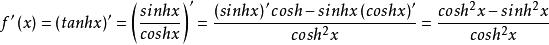雙曲正切函式
雙曲正切函式而
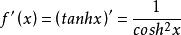雙曲正切函式 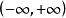雙曲正切函式得出雙曲正切函式的導數為： 。而無論x取何值，雙曲餘弦函式的值始終大於等於1，得出x在 內大於0，單調遞增。
凹凸性
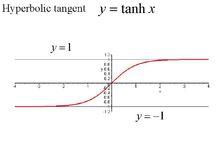雙曲正切函式的圖像
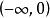雙曲正切函式
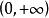雙曲正切函式雙曲正切函式在 上是凹函式，在 上是凸函式 。
根據定理：設f(x)在[a,b]上連續，在（a,b）內具有一階和二階導數，那么
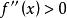雙曲正切函式（1）若在（a,b）內 ,則f(x)在[a,b]上的圖形是凹的。
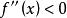雙曲正切函式（2）若在（a,b）內 ,則f(x)在[a,b]上的圖形是凸的。
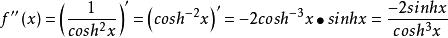雙曲正切函式則給雙曲餘弦函式二次求導，得
而雙曲餘弦函式恆大於0，而雙曲正弦函式在x<0時，它的值小於0，x>0時，它的值大於0，即得出上述結論。
