定義
雙曲拋物面又稱馬鞍面,它在笛卡兒坐標系中的方程為:
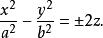 雙曲拋物面
雙曲拋物面其中x、y、z是平面直角坐標系三個坐標軸方向上的變數,a、b是常數。
幾何表示
如果把雙曲拋物面
 雙曲拋物面
雙曲拋物面順著+ z的方向鏇轉π/4的角度,則方程為:
 雙曲拋物面
雙曲拋物面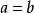 雙曲拋物面
雙曲拋物面如果 ,則簡化為:.
 雙曲拋物面
雙曲拋物面 雙曲拋物面
雙曲拋物面最後,設 ,我們可以看到雙曲拋物面
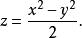 雙曲拋物面
雙曲拋物面與以下的曲面是全等的:
 雙曲拋物面
雙曲拋物面因此它可以視為乘法表的幾何表示。
雙曲拋物面圖像
 圖1.雙曲拋物面
圖1.雙曲拋物面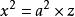 雙曲拋物面
雙曲拋物面 雙曲拋物面
雙曲拋物面 雙曲拋物面
雙曲拋物面 雙曲拋物面
雙曲拋物面 雙曲拋物面
雙曲拋物面用平面 截此曲面, 所得截痕l為平面 上的拋物線 ,此拋物線開口向下,其頂點坐標為 。當t變化時,l的形狀不變,位置只作平移,而l的頂點的軌跡L為平面y=0上的拋物線。因此,以l為母線,L為準線,母線l的頂點在準線L上滑動,且母線作平行移動,這樣得到的曲面便是雙曲拋物面。

