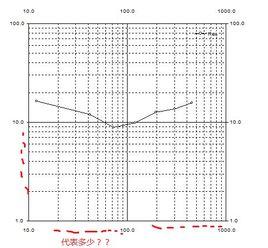
介紹
算術坐標系統
就是普通的笛卡兒坐標,橫縱的刻度都是是等距的。舉例來說:如果每1cm的長度都代表2,則刻度按照順序0,2,4,6,8,10,12,14……,但一般情況下,刻度表示仍然是均勻的,按照0,1,2,3,4的順序排下去。對應的實際意義,需要人們在腦子裡盤算,並不一定需要在坐標的刻度上直觀地表示出來。
對數坐標系統
坐標軸是按照相等的指數增加變化表示的。舉例來說:如果每1cm代表10的1次方增加,則坐標軸刻度的表示依次為1,10,100,1000,10000……
算數坐標系統較對數坐標系統,他們區別體現於等刻度值增長方式不同,一個均勻增長,一個對數增長。
雙對數坐標
指兩個坐標軸是對數坐標,即假如對應於x、y軸,則兩軸等刻度情況下,其值以相應底數成次方增長。
( 注意:在各自坐標軸上的是 真數 ,不是求對數後的值。)
舉例來說:如果每1cm代表10的1次方增加,則坐標軸刻度依次為1,10,100,1000,10000……
使用基本原則
在下列情況下套用對數坐標紙:
1)如果所研究的函式 y和自變數 x在數值上均變化了幾個數量級。例如,已知 x和 y的數據為: x= 10, 20, 40, 60, 80, 100, 1000, 2000, 3000, 4000 y= 2, 14, 40, 60, 80, 100, 177, 181, 188, 200 在直角坐標紙上作圖幾乎不可能描出在x的數值等於10、20、40、60、80時,曲線開始部分的點,但是若採用對數坐標紙則可以得到比較清楚的曲線(如圖3)。
2)需要將曲線開始部分劃分成展開的形式。
3)當需要變換某種非線性關係為線性關係時。
4)坐標軸的梯度選取要符合對數運算法則
套用範例
一般套用於冪函式。
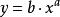 雙對數坐標
雙對數坐標原關係式:
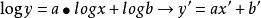 雙對數坐標
雙對數坐標取對數:
原關係式描繪出來是非線性的,不直觀,而取對數後就成為線性關係。
優點
1)可以直觀的通過判斷函式圖像是不是線性的,從而判斷函式是不是一個冪函式。
2)通過直線擬合就能得到 a的數值了。