定義
在積分學中, 橢圓積分最初出現於橢圓的弧長有關的問題中。Guilio Fagnano和歐拉是最早的研究者。現代數學將 橢圓積分定義為可以表達為如下形式的任何函式f的積分
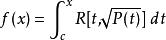 橢圓積分
橢圓積分其中R是其兩個參數的有理函式,P是一個無重根的3或4階多項式,而c是一個常數。
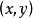 橢圓積分
橢圓積分通常,橢圓積分不能用基本函式表達。這個一般規則的例外出現在P有重根的時候,或者是R,沒有 y的奇數冪時。但是,通過適當的簡化公式,每個橢圓積分可以變為只涉及有理函式和三個經典形式的積分。(也即,第一,第二,和第三類的橢圓積分)。
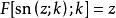 橢圓積分
橢圓積分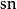 橢圓積分
橢圓積分除下面給出的形式之外,橢圓積分也可以表達為勒讓德形式和Carlson對稱形式。通過對施瓦茨-克里斯托費爾映射的研究可以加深對橢圓積分理論的理解。歷史上,橢圓函式是作為橢圓積分的逆函式被發現的,特別是這一個:其中是雅可比橢圓函式之一。
記法
橢圓積分通常表述為不同變數的函式。這些變數完全等價(它們給出同樣的橢圓積分),但是它們看起來很不相同。很多文獻使用單一一種標準命名規則。在定義積分之前,先來檢視一下這些變數的命名常規:
 橢圓積分
橢圓積分模角
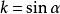 橢圓積分
橢圓積分橢圓模;
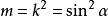 橢圓積分
橢圓積分參數;
上述三種常規完全互相確定。規定其中一個和規定另外一個一樣。橢圓積分也依賴於另一個變數,可以有如下幾種不同的設定方法:
 橢圓積分
橢圓積分幅度
 橢圓積分
橢圓積分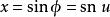 橢圓積分
橢圓積分其中
 橢圓積分
橢圓積分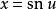 橢圓積分
橢圓積分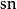 橢圓積分
橢圓積分,其中而是雅可比橢圓函式之一
 橢圓積分
橢圓積分 橢圓積分
橢圓積分規定其中一個決定另外兩個。這樣,它們可以互換地使用。注意也依賴於 m。其它包含的關係有
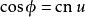 橢圓積分
橢圓積分和
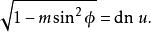 橢圓積分
橢圓積分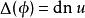 橢圓積分
橢圓積分後者有時稱為 δ幅度並寫作。有時文獻也稱之為補參數,補模或者補模角。這些在四分周期中有進一步的定義
第一類不完全
第一類不完全橢圓積分F定義為
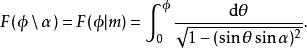 橢圓積分
橢圓積分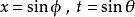 橢圓積分
橢圓積分與此等價,用雅可比的形式,可以設;則
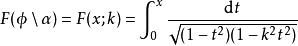 橢圓積分
橢圓積分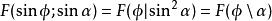 橢圓積分
橢圓積分其中,假定任何有豎直條出現的地方,緊跟豎直條的變數是(如上定義的)參數;而且,當反斜槓出現的時候,跟著出現的是模角。 在這個意義下,,這裡的記法來自標準參考書Abramowitz and Stegun。
但是,還有許多不同的用於橢圓積分的記法。取值為橢圓積分的函式沒有(象平方根,正弦和誤差函式那樣的)標準和唯一的名字。
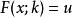 橢圓積分
橢圓積分注意
其中u如上文所定義:由此可見,雅可比橢圓函式是橢圓積分的逆。
加法公式
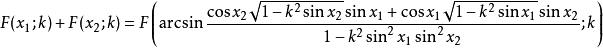 橢圓積分
橢圓積分導數
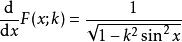 橢圓積分
橢圓積分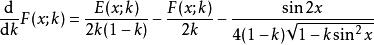 橢圓積分
橢圓積分第二類不完全
第二類不完全橢圓積分E是
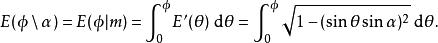 橢圓積分
橢圓積分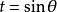 橢圓積分
橢圓積分與此等價,採用另外一個記法(作變數替換),
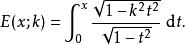 橢圓積分
橢圓積分其它關係包括
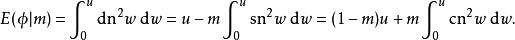 橢圓積分
橢圓積分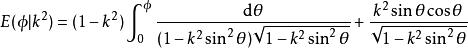 橢圓積分
橢圓積分加法公式
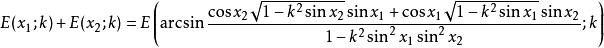 橢圓積分
橢圓積分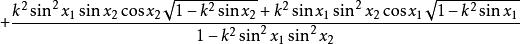 橢圓積分
橢圓積分性質
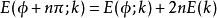 橢圓積分
橢圓積分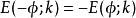 橢圓積分
橢圓積分導數
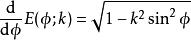 橢圓積分
橢圓積分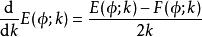 橢圓積分
橢圓積分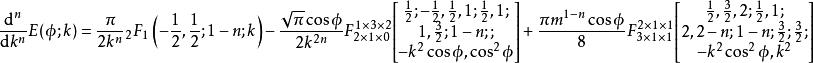 橢圓積分
橢圓積分第三類不完全
 橢圓積分
橢圓積分第三類不完全橢圓積分是
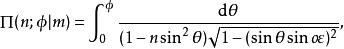 橢圓積分
橢圓積分或者
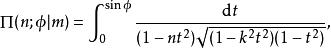 橢圓積分
橢圓積分或者
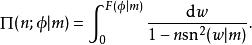 橢圓積分
橢圓積分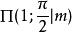 橢圓積分
橢圓積分數字n稱為 特徵數,可以取任意值,和其它參數獨立。但是要注意對於任意m是無窮的。
第一類完全
第一類完全橢圓積分K(k)
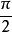 橢圓積分
橢圓積分如果幅度為或者 x=1,則稱橢圓積分為 完全的。 第一類完全橢圓積分K可以定義為
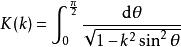 橢圓積分
橢圓積分或者
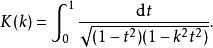 橢圓積分
橢圓積分它是第一類不完全橢圓積分的特例:
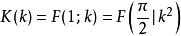 橢圓積分
橢圓積分第一類完全橢圓積分有時稱為四分周期。它可以利用算術幾何平均值來快速計算。
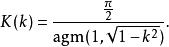 橢圓積分
橢圓積分第二類完全
第二類完全橢圓積分E(k)
第二類完全橢圓積分E可以定義為
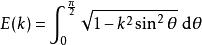 橢圓積分
橢圓積分或者
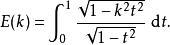 橢圓積分
橢圓積分它是第二類不完全橢圓積分的特殊情況:
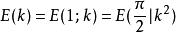 橢圓積分
橢圓積分第三類完全
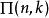 橢圓積分
橢圓積分不同 n值的第三類完全橢圓積分
 橢圓積分
橢圓積分第三類完全橢圓積分可以定義為
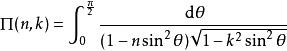 橢圓積分
橢圓積分注意有時第三類橢圓積分被定義為帶相反符號的n,也即
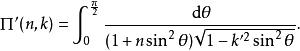 橢圓積分
橢圓積分函式關係
勒讓得關係:
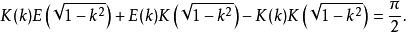 橢圓積分
橢圓積分
