概念
一個階梯函式就是一個分段常值函式,只是含有的階段很多但是有限。
 階梯函式
階梯函式 階梯函式
階梯函式 階梯函式
階梯函式 階梯函式
階梯函式 階梯函式
階梯函式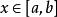 階梯函式
階梯函式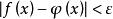 階梯函式
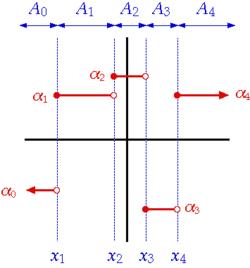
階梯函式定義在上的數值函式是階梯函式,是指對任意的,存在上的一個階台函式,使得對任意的,有。
 階梯函式
階梯函式 階梯函式
階梯函式 階梯函式
階梯函式 階梯函式
階梯函式 階梯函式
階梯函式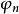 階梯函式
階梯函式於是說被一致地逼近,誤差為。這相當於說,所謂是階梯函式,是指是一致收斂的階台函式的序列的(一致)極限。
 階梯函式
階梯函式 階梯函式
階梯函式 階梯函式
階梯函式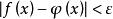 階梯函式
階梯函式如果是階梯函式,則是有界的。實際上,從對任意的成立的,得
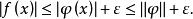 階梯函式
階梯函式代數性質
 階梯函式
階梯函式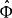 階梯函式
階梯函式性質1:在上的階梯函式形成一矢量空間,這空間用來表示。
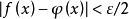 階梯函式
階梯函式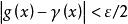 階梯函式
階梯函式這個性質是明顯的。例如,從,,得
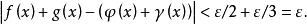 階梯函式
階梯函式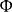 階梯函式
階梯函式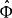 階梯函式
階梯函式還要指出,是的子空間。
 階梯函式
階梯函式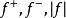 階梯函式
階梯函式性質2:如果是階梯函式,則也是階梯函式。
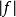 階梯函式
階梯函式只須對做證明即可;這性質來自
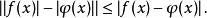 階梯函式
階梯函式 階梯函式
階梯函式 階梯函式
階梯函式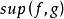 階梯函式
階梯函式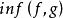 階梯函式
階梯函式結果是,對兩個(或有限多個)階梯函式,,函式,也是階梯函式。
 階梯函式
階梯函式 階梯函式
階梯函式性質3:如果是正階梯函式或零,則存在一個正階台函式或;零的序列,一致收斂到。
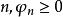 階梯函式
階梯函式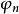 階梯函式
階梯函式 階梯函式
階梯函式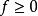 階梯函式
階梯函式 階梯函式
階梯函式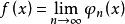 階梯函式
階梯函式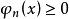 階梯函式
階梯函式首先提出,如果對任意的;又如果收斂到,則。這是因為對一切,且。
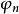 階梯函式
階梯函式 階梯函式
階梯函式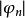 階梯函式
階梯函式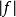 階梯函式
階梯函式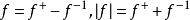 階梯函式
階梯函式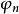 階梯函式
階梯函式從上面性質2得到,如果一致收斂到,則同時有也一致收斂到。可是對一切數值函式有,由此對使用加法有
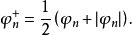 階梯函式
階梯函式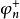 階梯函式
階梯函式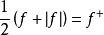 階梯函式
階梯函式 階梯函式
階梯函式 階梯函式
階梯函式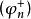 階梯函式
階梯函式 階梯函式
階梯函式於是一致收斂到。特別地,如果,則且是一致收斂到的正階台函式的序列。