簡介
分段單調函式是若干個單調函式相接的函式。
分段單調函式的定義域可以分成有限個區間,在其中每一個區間上都是單調的一元函式。即:若存在區間[a,b]的分法a=x<x<x<…<x=b,使在每個小區間[x,x](i=1,2,...,n)上函式f(x)都是單調的,則稱f:[a,b]→R是分段單調的。
類型
階梯函式、單調函式都是分段單調函式。
階梯函式
一個階梯函式就是一個分段常值函式,只是含有的階段很多但是有限。
 分段單調函式
分段單調函式 分段單調函式
分段單調函式 分段單調函式
分段單調函式 分段單調函式
分段單調函式 分段單調函式
分段單調函式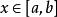 分段單調函式
分段單調函式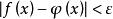 分段單調函式
分段單調函式定義在上的數值函式是階梯函式,是指對任意的,存在上的一個階台函式,使得對任意的,有。
 分段單調函式
分段單調函式 分段單調函式
分段單調函式 分段單調函式
分段單調函式 分段單調函式
分段單調函式 分段單調函式
分段單調函式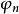 分段單調函式
分段單調函式於是說被一致地逼近,誤差為。這相當於說,所謂是階梯函式,是指是一致收斂的階台函式的序列的(一致)極限。
單調函式
一般的,不強調區間的情況下,所謂的單調函式是指, 對於整個定義域而言,函式具有單調性。而不是針對定義域的子區間而言。舉個例子,反比例函式是一個具有單調性的函式,而不是一個單調函式,因為在反比例函式的定義域上,並不呈現整體的單調性。單調函式只是單調性函式中特殊的一種。區間具有單調性的函式並不一定是單調函式,而單調函式的子區間上一定具有單調性。具有單調性函式可以根據區間不同而單調性不同。
