樣條函式

在數學學科數值分析中，樣條是一種特殊的函式，由多項式分段定義。樣條的英語單詞spline來源於可變形的樣條工具，那是一種在造船和工程製圖時用來畫出光滑形狀的工具。在中國大陸，早期曾經被稱做“齒函式”。後來因為工程學術語中“放樣”一詞而得名。 在插值問題中，樣條插值通常比多項式插值好用。用低階的樣條插值能產生和高階的多項式插值類似的效果，並且可以避免被稱為龍格現象的數值不穩定的出現。並且低階的樣條插值還具有“保凸”的重要性質。 在計算機科學的計算機輔助設計和計算機圖形學中，樣條通常是指分段定義的多項式參數曲線。由於樣條構造簡單，使用方便，擬合準確，並能近似曲線擬合和互動式曲線設計中複雜的形狀，樣條是這些領域中曲線的常用表示方法。

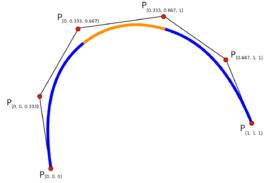
定義

給定k個點t，稱為 節點（knot），分布在一個區間[a,b]滿足

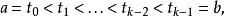樣條函式

一個參數曲線

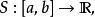樣條函式

稱為n次樣條，如果

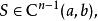樣條函式

並且在限制到每個子區間時，

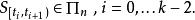樣條函式

換句話說，在每個子區間或者說 節點長度（knot span）

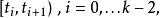樣條函式

S和一個n次多項式相同。

S（t） 稱為節點值而（t,S（t））稱為內部控制點（internal control point）. (t,...,t)稱為節點向量。如果節點等距分布在區間[a,b]上，我們稱樣條均勻（uniform），否則為非均勻（non-uniform）。

舉例

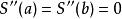樣條函式

樣條函式

最簡單的樣條是一次的，它也叫做線性樣條，或者多邊形。一般的樣條是自然的三次樣條。自然定義為樣條多項式的二階導數在插值區域的兩端相等。 在區間 ，這使得樣條在插值區間外為直線而不影響光滑程度。

註解

對於一個給定的節點向量，所有n次樣條構成一個向量空間。這個空間的一個基是n次B樣條基。

歷史

在計算機被使用之前，數字演算用手工完成。雖然分段定義的象signum函式或階梯函式這樣的函式也被用到，一般人更喜歡多項式因為它們比較容易算。隨著計算機的發展，樣條變得越來越重要。它們一開始是作為多項式在插值中的替代品，後來又作為在計算機圖形學中構造光滑和可變形狀的工具。

spline function是一類分段（片）光滑、並且在各段交接處也有一定光滑性的函式。簡稱樣條。樣條一詞來源於工程繪圖人員為了將一些指定點連線成一條光順曲線所使用的工具，即富有彈性的細木條或薄鋼條。由這樣的樣條形成的曲線在連線點處具有連續的坡度與曲率。分段低次多項式、在分段處具有一定光滑性的函式插值就是模擬以上原理髮展起來的，它克服了高次多項式插值可能出現的振盪現象，具有較好的數值穩定性和收斂性，由這種插值過程產生的函式就是多項式樣條函式。

樣條函式的研究始於20世紀中葉，到了60年代它與計算機輔助設計相結合，在外形設計方面得到成功的套用。樣條理論已成為函式逼近的有力工具。它的套用範圍也在不斷擴大，不僅在數據處理、數值微分、數值積分、微分方程和積分方程數值解等數學領域有廣泛的套用，而且與最優控制、變分問題、統計學、計算幾何與泛函分析等學科均有密切的聯繫。

參看

•樣條插值

•厄爾密樣條（Hermite spline）

•B樣條

•非均勻有理B樣條（Non uniform rational B-spline，NURBS）

•de Boor算法

•貝塞爾樣條