簡介
基本算術
基本算術中,除法指將一個集合中的物件分成若干等份。例如,10個蘋果平分給5人,每人可得10/5 = 2個蘋果。同理,10個蘋果只分給1人,則他/她可得10÷1 = 10個蘋果。
若除以0又如何?若有10個蘋果,無人來分,每“人”可得多少蘋果?問題本身是沒有意義的,根本無人來,談論每“人”可得多少根本多餘。所以,10÷0,在基本算術中,是無意義或未下定義的。
另一種解釋是將除法理解為不斷的減法。例如“13除以5”,換一種說法,13減去兩個5,餘下3,即被除數一直減去除數直至餘數數值低於被除數,算式為13÷5 = 2…3。若某數除以零,就算不斷減去零,餘數也不可能小於被除數,使得算式與無窮拉上關係,超出基本算術的範疇。
早期嘗試
婆羅摩笈多(598–668年)的著作Brahmasphutasiddhanta被視為最早討論零的數學和定義涉及零的算式的文本。但當中對除以零的論述並不正確,根據婆羅摩笈多,
"一個正或負整數除以零,成為以零為分母的分數。零除以正或負整數是零或以零為分子、該正或負整數為分母的分數。零除以零是零。"830年,摩訶吠羅在其著作 Ganita Sara Samgraha試圖糾正婆羅摩笈多的錯誤,但不成功:
"一數字除以零會維持不變。"婆什迦羅第二嘗試解決此問題。令 n/0=∞,雖然此定義有一定道理,但會導致悖論(參見下面)。
代數處理
若某數學系統遵從域的公理,則在該數學系統內除以零必須為沒有意義。這是因為除法被定義為是乘法的逆向操作,即a/b值是方程 b x = a中 x的解(若有的話)。若設 b = 0,方程式 bx = a可寫成 0 x = a或直接 0 = a。因此,方程 bx = a沒有解(當 a ≠ 0時),但 x是任何數值也可解此方程(當 a = 0時)。在各自情況下均沒有的數值,所以1未能下定義。
除以零的謬誤
在代數運算中不當使用除以零可得出無效證明:2 = 1
由:0×1=0,0×2=0,
得出0×1=0×2。
兩邊除以零,得出0×1/0=0×2/0。
化簡,得:1=2!
以上謬論一個假設,就是某數除以0是容許的並且0 / 0 = 1。
虛假的除法
在矩陣代數或線性代數中,可定義一種虛假的除法,設 a/ b= ab+,當中 b代表 b的虛構倒數。這樣,若 b存在,則 b = b;若 b等於0,則0 = 0。參見廣義逆。
數學分析
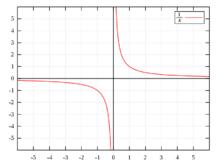 除以零
除以零對於函式 y=1/ x,當 x→0時,y→∞;反之亦然。
擴展的實數軸
表面看來,可以藉著考慮隨著 b趨向0的 a/ b極限而定義 a/0。 對於任何正數 a,
而對於任何負數 a,
所以,對於正數 a,a/0可被定義為+∞,而對於負數 a則可定義為-∞。不過,某數也可以由負數一方(左面)趨向零,這様,對於正數 a, a/0定義為-∞,負數 a定義為+∞。由此可得(假設實數的基本性質可套用在極限上):
最終變成 +∞ = −∞,與在擴展的實數軸上對極限賦予的標準定義不相符。辦法是用沒有正負號的無限,參見下面。
另外,利用極限的比無為0/0提供解釋:
並不存在,而
若隨著 x趨向0, f( x)與 g( x)均趨向0,該極限可等於任何實數或無限,或者根本不存在,視乎 f及 g是何函式(參閱洛必達法則)。由此,0/0難以被定義為一極限。
無限接近法
2/0.1=20,2/0.01=200,2/0.001=2000,2/0.000001=2000000,……
愈接近0,所得的數愈大,所以除以0個數會變做無限大。
黎曼球
集合 C∪{∞}為黎曼球(Riemann sphere),在複分析中相當重要。

