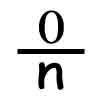定義
分子為0(分母不為0)的分數即為零分數。
舉例
(1)當m=0時,m/n=0/n=0。即:當分子是0時,分數值等於0。
例如:0/7=0。
(2)當n=1時,m/n=m/1=m。即:當分母是1時,分數值就是分子。根據補充定義,任何整數m都可以用m/1來表示,從這個意義上講,整數是特殊的分數,整數集是分數的真子集。
例如:5=5/1;0/1=0。
意義
套用意義
1. 零作分母時無意義,零作分子時有意義,但所得結果永遠是零。
例:0/5 :把單位“1”平均分成5份,取其中0份,等於0,即 0/5=0
(註:零分數隻出現在分數加減法中,一般是很少見的。)
2.零分數不參與分數的分類。真分數集中分布在0和1之間的線段上,假分數分布在直線上1或1的右邊。”由此我們可以知道:真分數只是集中分布在0和1之間的線段上,它大於0而小於1,分布在直線0上的分數不是真分數。假分數的定義為:“分子比分母大或者分子和分母相等的分數,叫做假分數。假分數大於1或等於1。”很顯然,0/7也不是假分數。通過上面的分析,我們可以知道,
0/5一類數不是真分數,它是一種特殊的分數,是零分數。
數學意義
從分數的意義中可以看出“零分數”和“分數形式的整數”都是分數的一種特殊形式。
由其是“零分數”,在數學理論中,是把它做為一個數學概念出現的。即:分子是零的分數叫做零分數。
“零分數”的實際意義是整數“0”的分數表現形式。它的本質是整數。由其是“0”在數學運算中有著它特殊性質,在很多數學概念中對“0”都要做明確的限定。
在分數與倒數的矛盾點上應該對“零分數”做同樣的限定,在這裡邊應該有兩處有明確的限定:
(1)根據倒數的定義可知,求一個數的倒數(0除外――因為0不能做除數,所以0沒有倒數),就是1除以這個數所得的數。
(2)為了簡便,求一個分數(零分數除外)的倒數,調換一下這個分數的分子與分母的位置就可以。