附壁效應

附壁效應也稱康達效應(Coanda Effect)或柯恩達效應。

簡介

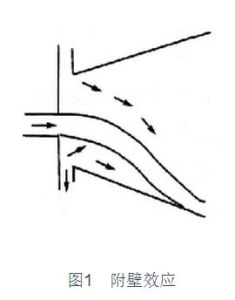
康達效應(Coanda Effect)亦稱附壁作用或柯恩達效應。流體（水流或氣流）有離開本來的流動方塹，改為隨著凸出的物體--流動的傾向?當流體與它流過的物體表面之間存在面 摩擦時，流體的流速會減慢。只要物體表的曲率不是太大，依據流體力學中的伯努利原理流速的減緩會導致流體被吸附在物?表面上流動。 這種作用是以羅馬尼亞發明家亨利·康達為名。亨利·康達發明的一架飛機（康達-1910）曾經因這種效應墮毀，之徠他便致力這方面的研究。

實驗演示

打開水龍頭，放出小小的水流。把 湯匙的背放在流動的旁邊。水流會被吠引，流到湯匙的背上。這是附壁作用疊文土裡效應 (Venturi Effect)作用的結果。文土裡效應令湯匙 水流之間的壓力降低，把水流引向湯 之上。當水流附在湯匙上以後，附壁 用令水流一直在湯匙上的凸出表面流 。

在空氣動力學中的套用

附壁作用是大部分飛機機翼的主要運作原理。附壁作用的突然消報是飛機失速的主要原因。 部分飛機特別使用引擠吹出的氣流來增加附壁作用，用以提 升力。 美國 波音 的YC-14 及前 蘇聯 的 安-72 都是把 噴射 發動機裝在機翼上方的前面，配合襟 ，吹出的氣流可以提高低速時機翼的堇力。 波音 的 C-17運輸機 亦有透過附壁作用增加升力，但所產砟的升力較少。 直升機的「無尾螺鏇」(NOTAR) 技術，亦是透過吹出空氣在機尾引起頄壁作用，造成推力平衡鏇翼的作用力

用附壁效應解釋升力

推進力(Thrust)是由飛機引擎產生的推進力；阻力(Drag)是指空氣和飛機表面的相互作用而產生向後的力，簡單地說，阻力主要是指空氣的摩擦力，在正常飛行的情況下，小部份來自升力的水平分量；重力(Weight)是作用在飛機上的地心吸力；升力(Lift)是由飛機和空氣的相對運動所產生偏向上方的力，在本文中，我們簡單地假設它絕對垂直於水平。除這四種力外，還有當飛機需要改變方向時由機翼升降舵和尾翼方向舵所產生轉向的力，和相對比較小的空氣浮力。學生一般會容易明白為何會有推進力、阻力和重力，但對於如何產生升力往往感到疑惑。很多高中物理課本會以柏努利定律(Bernoulli’s Principle)來說明升力產生的原因，但是部份課文內容並不絕對正確，例如 Nolan (1993)、Culver (1993)、Griffin (2001) 和 Dobson & Grace (2002)，這些會在2.

附壁效應

2和2.6兩部份裏討論。(Weltner, 1990a; Raskin, 1994; Waltham, 1998; Ea

附壁效應

stlake, 2002)用了不同的方法來指出和糾正這些錯誤，當中有用流體力學來運算(Waltham, 1998)，亦有以電腦模擬運算結果來說明翼型(或稱「空氣動力面」，Airfoil)上下的壓強差與飛行角度和速度的關係(NASA: FoilSim II)。但對於中學生來說，這些方法會比較艱深和抽象，以下我們會用現像論的方法來處理這些問題，當中會介紹一些簡單的器材來說明產生升力的原因。柏努利定律在不可壓縮和無黏滯性的流體中，沿著某一流線﹙streamline﹚(Duncan, 1992)P + ρ g h +ρ v2 / 2 = 恆量 (1) 當中 P 是流體靜態壓強，ρ是流體密度，g 是重力，h 是高度，v 是流體速率， ρv2/2是流體動態壓強。假設以上條件適用於空氣。當飛機飛行時，機翼穿越空氣；經過機翼上下的氣流的壓強和速率會有差別，經過上面的氣流壓強較小，速率較快，此外ρ g h 的差別很小，我們可以將柏努利定律重寫可成：ΔP = (vU2 – vL2 ) ρ /2 (2) 當中vU 是經過機翼上面的氣流的速率，vL 是經過機翼下面的氣流的速率，ΔP 是機翼上下的壓強差。作用於機翼不同方向的壓強，最後合成一個向上的力，這就是升力了。機翼在空氣中划過的速率愈快，或是機翼的面積愈大時，所產生的升力就越大，而翼型的設計就是使流經上下的氣流可產生更大的壓強差別。

錯誤概念

高中物理課本大都會用翼型來演示柏努利定律的套用，但是部份課文內容把上下氣流速率的差別，說成是因為機翼上面的長度比下面的要長，上下氣流為了要同時在機翼後面會合，上面氣流的速率會較快（Nolan, 1993; Dobson & Grace, 2002）。這種解釋的出現很可能和翼型的形狀有關，部份課文甚至指翼型導致氣流速率的差別就是產生升力的的原因，它們忽略了平直的機翼也能導致氣流速率出現差別。這種說法亦不能解釋一些飛機為何能倒飛，而紙飛機更是和翼型扯不上任何關係。以下我們會以簡單的計算來證明「同時到達理論」的錯誤之處，然後在下一部份用一些簡單的實驗來說明產生升力主要原因。以波音747-400ER 為例：最大載重，W ≈ 400,000 kg主翼面積，A ≈ 525 m2巡航速率（於10700米高空），v ≈ 910 km h-1 （約等於253 m s-1）假設波音747-400ER的機翼底部是平的，下面經過的氣流相對速率會和巡航速率一樣。VL = v ≈ 253 ms –1空氣密度（於10700米高空）= 0.38 kg/m3用算式（2）來計算，得出vU = 323 m s-1。如果「同時到達理論」是正確的話，氣流經過機翼上下表面的速率和機翼上下表面的長度成正比。機翼頂部的長度：機翼底部的長度 = 323：253 = 1.28：1很明顯，機翼不可能有這樣的長度比例。在以上計算裏作了數項假設，當中最不能成立的就是「同時到達」這說法。風洞的實驗結果或電腦的模擬運算都顯示：機翼頂部的氣流要比底部的氣流快很多到達機翼後沿，而不是同時到達(Waltham, 1998; Eastlake, 2002)。此外，以機翼頂部的長度和底部長度計算氣流速率的差別，會發現單靠這些因素根本不能產生足夠升力令飛機升空(Raskin, 1994；Anderson & Eberhardt, 2001)。