介紹
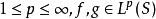閔科夫斯基不等式
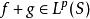閔科夫斯基不等式在數學中， 閔可夫斯基不等式（Minkowskiinequality）表明L空間是一個賦范向量空間。設S是一個度量空間， ，那么 ，我們有：
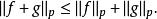閔科夫斯基不等式
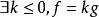閔科夫斯基不等式
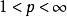閔科夫斯基不等式如果 ，等號成立若且唯若，或者g=kf。
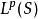閔科夫斯基不等式閔可夫斯基不等式是 中的三角不等式。它可以用赫爾德不等式來證明。和赫爾德不等式一樣，閔可夫斯基不等式取可數測度可以寫成序列或向量的特殊形式：
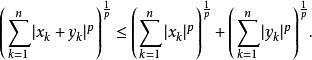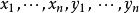閔科夫斯基不等式
閔科夫斯基不等式
閔科夫斯基不等式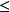
閔科夫斯基不等式
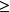閔科夫斯基不等式將所有實數（n為S的維數）改成複數同樣成立。值得指出的是，如果 ，則 可以變為 。
積分形式的證明
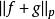閔科夫斯基不等式我們考慮 的p次冪：
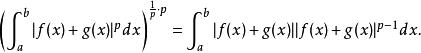閔科夫斯基不等式（用三角形不等式展開|f(x)+g(x)|）
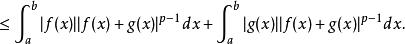閔科夫斯基不等式（用赫爾德不等式）
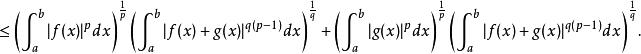閔科夫斯基不等式
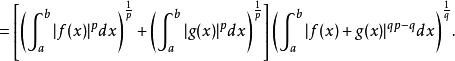閔科夫斯基不等式
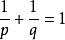閔科夫斯基不等式（利用 p=qp-q，因為）
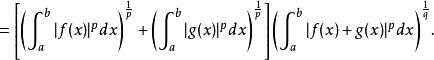閔科夫斯基不等式現在我們考慮這個不等式序列的首尾兩項。首項除以尾項的最後一個因子，即得
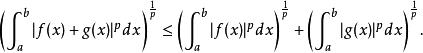閔科夫斯基不等式這正是我們所要的結論。對於序列的情形，證明是完全類似的。
參閱
•馬勒不等式
