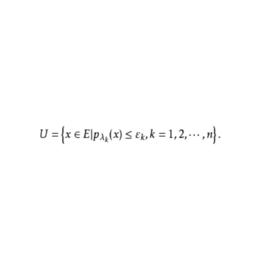拓撲線性空間
拓撲線性空間（topological）是一類具有拓撲結構的線性空間。如果實數域或複數域 K 上的線性空間E同時是有拓撲 τ 的拓撲空間，並且線性空間的基本運算x+y和αx（x，y∈E，α∈K）分別作為E×E和K×E到E中的映射按 τ 是連續的，則稱E為（實或復）拓撲線性空間或拓撲向量空間。而 τ 稱為E的線性拓撲或向量拓撲，零元的均衡的領域全體組成零元的鄰域基。滿足T分離公理的拓撲線性空間是完全正則的。
拓撲線性空間理論是泛函分析的一個重要分支，其基本概念建立於20世紀30年代，而今已經發展成為一門完整的學科，在純粹數學和套用數學、理論物理、現代理學和現代工程理論中都有廣泛套用。
局部凸空間
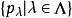自反局部凸空間
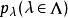自反局部凸空間局部凸空間（locally convex space）是最重要的一類拓撲線性空間。設E是拓撲線性空間，如果E中存在由均衡凸集組成的零元的鄰域基，就稱E是局部凸的拓撲線性空間，簡稱局部凸空間，而E的拓撲稱為局部凸拓撲。零元的每個均衡凸鄰域V的閔科夫斯基泛函 p(x) 是E上的連續半範數。反之，設是E上一族半範數，E上使均為連續的最弱拓撲是局部凸的，且零元的均衡凸鄰域基由下面形式的集組成
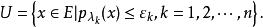自反局部凸空間
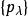自反局部凸空間
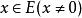自反局部凸空間
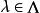自反局部凸空間
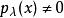自反局部凸空間 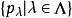自反局部凸空間
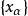自反局部凸空間
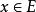自反局部凸空間
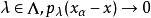自反局部凸空間這個局部凸拓撲稱為由半範數族確定的局部凸拓撲。如果對任何，都存在使，則確定的局部凸拓撲是豪斯多夫拓撲。通常局部凸空間都指豪斯多夫局部凸空間。E中的定向半序點列收斂於等價於對每個。
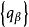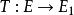自反局部凸空間
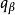自反局部凸空間
自反局部凸空間
自反局部凸空間設E是由另一半範數族確定的局部凸空間，則使線性映射連續的充分必要條件是，對任意的，總存在有限個和常數c，使不等式
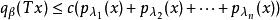自反局部凸空間 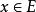自反局部凸空間對一切成立。
局部凸空間的完備化空間也是局部凸的。根據哈恩-巴拿赫泛函延拓定理，局部凸空間上存在足夠多的非零連續性泛函。正因為如此，局部凸空間理論成為拓撲線性空間理論中最重要的部分。
關於局部凸空間理論的發展大約是始於迪厄多內（Dieudonné，J.）和施瓦茲（Schwarz，L.）在1949年的工作，它的一個主要推動力是分布理論，即廣義函式理論。
自反局部凸空間
自反局部凸空間(reflexive locally convex space)屬於一類局部凸空間。設E是局部凸空間，則賦予強拓撲的共扼空間E'的共扼空間E''包含原來的空間E，當E" = E時，稱E是半自反的。進一步當E的拓撲和強拓撲β(E,E')一致時，稱E為自反的。E為半自反的充分必要條件是E的任意有界弱閉凸集是弱緊的。E為自反的充分必要條件是E為半自反的且是擬桶型的。對於賦可列范線性空間，自反和半自反是一致的。
擬桶型空間
擬桶型空間（quasi-barreled space）是桶型空間概念的推廣。設E是局部凸空間，E中的子集A稱為擬桶集，是指A是吸收一切有界集的桶集。如果E中每個擬桶集都是零元的鄰域，則稱E為擬桶型空間。局部凸空間為擬桶型空間的充分必要條件是在每個有界集上的下半連續半範數是連續的。
