簡介
閔科夫斯基泛函是拓撲線性空間上的一類非負值函式,是研究凸集的有效工具。
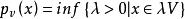 閔科夫斯基泛函
閔科夫斯基泛函設E是線性空間,V是E中凸吸收子集,E上如下定義的實值泛函稱為關於V的閔科夫斯基泛函。
性質
閔科夫斯基泛函p(・)是E上的次可加泛函,而且當V是均衡凸吸收集時,p(・)是半範數。
泛函
泛函是數學中重要的基本概念,是現代數學的重要研究對象之一,也是數學與其它領域研究與套用的一個重要工具。簡單的說,泛函就是定義域是一個函式集,而值域是實數集或者實數集的一個子集,推廣開來, 泛函就是從任意的向量空間到標量的映射。也就是說,它是從函式空間到數域的映射。
設{y}是給定的函式集,如果對於這個函式集中任一函式y(x) 恆有某個確定的數與之對應,記為П(y(x)),則П(y(x))是定義於集合{y(x)}上的一個泛函。
泛函定義域內的函式為可取函式或容許函式, y(x) 稱為泛函П的變數函式。
拓撲線性空間
 閔科夫斯基泛函
閔科夫斯基泛函設X為實數域或複數域K上的線性空間,是X上的拓撲,如果
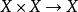 閔科夫斯基泛函
閔科夫斯基泛函(1)加法是的連續映射;
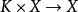 閔科夫斯基泛函
閔科夫斯基泛函(2)數乘是的連續映射;
 閔科夫斯基泛函
閔科夫斯基泛函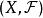 閔科夫斯基泛函
閔科夫斯基泛函則稱是X上的向量拓撲或線性拓撲,稱為 拓撲線性空間或拓撲向量空間。
註:1)零元的均衡的鄰域全體組成零元的鄰域基。
2)滿足T分離公理的拓撲線性空間是完全正則的。
