簡介
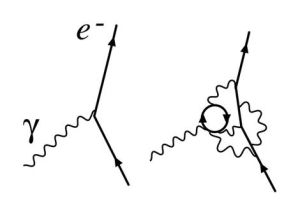量子電動力學中的重整化：此例為簡單的電子-光子互動作用，在一個重整化點決定了電子的電荷。實際上，可以在右圖看到包含了在其他點更多複雜的互動作用。重整化（Renormalization）是量子場論中解決紫外發散的一種方法。在量子場論發展的早期，在量子場論發展的早期，人們發現許多圈圖（即微擾展開的高階項）的計算結果含有發散（即無窮大）項。重整化是解決這個困難的一個方案。一個理論如果只有有限種發散項，則可以在拉氏量中引進有限數目的項來抵消這些無窮大項，這種情形被稱為可重整。反之，如果理論中有無限種發散項，則稱為不可重整。
自洽性要求
量子電動力學中的重整化：此例為簡單的電子-光子互動作用，在一個重整化點決定了電子的電荷。實際上，可以在右圖看到包含了在其他點更多複雜的互動作用。可重整化曾被認為一個場論所必需滿足的自洽性要求。它在量子電動力學和量子規範場論的發展過程中起過重要的作用。粒子物理的標準模型也是可重整的。
重整化只是聯繫不同能標下理論的一種方法
人們發現許多圈圖（即微擾展開的高階項）的計算結果含有發散（即無窮大）項。重整化是解決這個困難的一個方案。一個理論如果只有有限種發散項，則可以在拉氏量中引進有限數目的項來抵消這些無窮大項，這種情形被稱為可重整。反之，如果理論中有無限種發散項，則稱為不可重整。可重整化曾被認為一個場論所必需滿足的自洽性要求。它在量子電動力學和量子規範場論的發展過程中起過重要的作用。粒子物理的標準模型也是可重整的。現代場論的觀點認為所有理論都只是有效理論，它們都有它們的適用範圍。除了所謂的終極理論，所有理論在原則上都是不可重整的。在這種觀點下，重整化只是聯繫不同能標下理論的一種方法。
量子場論中的路徑積分
（學Peskin的書的話，正規化與重整化在介紹路徑積分以前就已經出現了，是通過Dylson展開來得到Feynman規則與Feynman圖的，隨後在第九章再用路徑積分的觀點重述一遍）。
路徑積分
說白了就是把從初態到末態的所有可能狀態都經歷一遍並求和的一種方法，是對作用量的e指數（帶i）的泛函積分。
而在場論中我們最感興趣的就是相互作用過程中的所謂S矩陣（當然，如果再考慮我們需要的是振幅平方而非振幅的話，那還能對S矩陣做簡化，得到所謂的“Cut圖”），而這個S矩陣可以用關聯函式（或者頂角函式，是去掉外線的關聯函式）來表達，而關聯函式（也所以頂角函式）則可以通過路徑積分來求出——找出生成泛函（和前面說的那個泛函積分有關），然後對N點關聯函式就取N個泛函微分。從而也就是說，一旦生成泛函知道了，那么你就可以知道關聯函式與頂角函式，那么從而你也就知道的S矩陣——也即散射截面。而這個生成泛函則是作用量的泛函積分。因而在量子場論中，作用量決定一切。在FreeField的路徑積分中，沒什麼大的問題，最後一般都能得到Gaussian積分（比如KG方程、Dirac方程等等），從而得到一個確定的解析結果。
微擾展開
但是在有外場的情況下就不同了。以Phi4理論為例，其中的外場可以寫為：V=g/4!*phi^4，因而將破壞泛函積分中的Gaussian型，從而無法簡單地得到解析解。
這個時候就需要利用微擾展開。以Phi4理論為例，外場V的作用是對Free作用量加上V的修正，而在生成泛函中作用量是在e指數上的，因而外場就是對Free生成泛函的exp(∫iV)修正（這裡需要將V中的參量修改為泛函微分算符，否則這一項需要算入泛函積分中，不能獨立出來）。由於這個e指數是一個算符，因而直接計算無法完成，從而就可以用Taylor展開來做微擾展開（為什麼是“微擾”，這個是高數問題了，這裡就不廢話了）。這個過程與Dylson展開（利用正規排序等手續）的結果是完全相同的。微擾展開以後，我們就得到了一系列（無窮多個）路徑積分的泛函微分，每一個都可以對應一張“Feynman圖”。Feynman圖與Feynman規則的好處就在於節約了你計算泛函微分的時間，直接用畫圖來代替計算，這是一個很好的方法（讓我想到了我高中數學老師的名言：遇到問題，想不出來，就考慮數形結合）。當然，Feynman圖中無法直觀表達出來的就是“對稱化因子”，不過這個可以通過對圖幾何性質的分析來計算——一個排列組合問題。好了，說道這裡還沒重整化什麼事，但是這是進入重整化所必須知道的鋪墊。
發散
在微擾展開以後，我們得到了很多路徑積分，或者說傳播子。其中有一些的結構很好：從初態開始，然後分叉，然後與別的傳播子匯合，進入末態。這種成為“樹圖”。但是另外一些就很不好了，比如在某些圖中會出現一個個“圈”，這種成為“圈圖”。比如Phi4理論中的2點關聯函式（一個粒子的初態末態）在一階微擾（零階微擾就是Free傳播子）中含有“真空泡”，就是一個直線的傳播子上獨立出來一個圈，圈與直線傳播子交於一點。這個真空泡就是Phi4的自作用勢能V給出的。這個圈對應了一個積分：i/(p^2-m^2)在整個p能取值的（四維）空間中的積分。顯然，這個積分是二次發散的。這就是量子場論中的一個重大問題：發散。
當紫外發散
然，並不是所有圈都可能發散，這有一個判斷標準。不過，無論如何，所有的量子場論都面對這種形式的發散問題。而這個發散的出現，則是由於上述積分允許跑遍全（相）空間，從而在無窮遠處的積分為發散——注意，在極點附近的積分是不發散的。事實上可以通過Wick轉動來消除這種極點對計算帶來的困擾——這是一種高數中介紹過的技巧。因而，量子場論在高能區（動量取大值）是發散的，這就是紫外發散。
這就是重整化
正規化
隨後，物理學家們為了計算這個發散的有效部分——也就是扣除發散以後的部分——而發明了“正規化”。正規化不能消除發散，但是可以得到除發散以外的有意義部分。正規化的方法有很多，早期主要是動量階段，也就是認為動量不能取到無窮大，而只能取到某一個有限值。這個思想在LQG中有所繼承，因為LQG中時空具有最小量子間隔，（通過Heinsenberg關係）對應到一個最大動量。這種正規化方案成為“動量階段正規化”，或者就稱為“Cut-off正規化”。後來，t’Hooft提出了維度正規化，並且一直沿用到現在，是比動量截斷更方便採用的方法。這個在標度相對論中有所繼承。當然，還有各種各樣的不同的正規化方案。所有這些正規化方案在扣除無限大發散以後得到的有效部分，是幾乎相同的。這不由讓人為想到：這些無窮大是否是由於某些未知的因素導致的“計算錯誤”？因而只要將這些錯誤扣除，我們得到的就是正確的理論了——這就是重整化。
重整化是建立在正規化的基礎上的，而且和正規化一樣，重整化方案也是有很多的。對應到維度正規化，我們採用的最多的是最小減除重整化法——只把那些發散扣除。
重整化的基本思想
就是在作用量中加上一些“抵消項counterterm”，從而使得最後的計算結構是有限的，而且能與我們的實驗結果相匹配。還是以Phi4理論為例，我們需要加上三個抵消項：質量抵消項、場重標度項和跑動耦合常數。
其中，質量抵消項直接將計算中的無窮大扣除。場重標度項則保證了傳播子可以得到正確的在殼條件和留數（有限發散點，也就是m^2處的留數，高數概念），而跑動耦合常數則保證了相互作用強度與我們的實驗能對應起來。
其中，在Phi4理論的一圈圖重整化中，質量抵消項是一個發散項，場重標度項與初末態動量無關，而跑動耦合常數則是依賴與初末態的——這也就是“跑動”一詞的由來。
重整化以後的理論不發散，而且能與實驗進行比較，從而可以得到相應的正確觀測量。而其跑動耦合常數則告訴我們：在不同的能量環境中，物理客體的性質是會發生變化的。這點後來在夸克幽閉等物理難題中得到了很好的套用，而標度相對論中則將這個觀點與分形進行了結合。
重要思想指導
當然，重整化也是有值得繼續思考的地方的。我們做重整化的一個重要思想指導，就是說一個物理理論應該是不發散的，而我們的場論由於沒有考慮高能物理，或者說我們還不知道高能物理，所以得到了發散結果。而重整化是一種將這些我們還不知道的高能機制“模糊”掉的方法，也即雖然我們不知道高能物理到底是什麼，但是其在計算中應該如何體現出來我們是清楚的——體現在保留的有限部分中。因而，一個重整化的理論是有效的，但並不是最終正確的。最終正確的理論肯定是不包含重整化的——因為能解釋高能行為。
重整化只不過是一種數學技巧
當然，還有一種觀點則是認為這裡的無限大發散完全是來源於微擾展開。就好比我們對1/(1-x)做微擾展開，得到1+x+x^2+x^3….，其收斂半徑為|x|<1，因而一旦我們在展開式中取x=2，那么這個微擾展開就會發散。因而有人有觀點認為：場論本身是收斂的，但是微擾展開以後是發散的，這完全是我們所採用的數學方法的問題，從而重整化只不過是一種數學技巧，並沒有新的物理內涵。
QED與實驗的符合程度
這兩個觀點到底誰對誰錯現在很難說，因為非微擾的處理方法我們現在沒有，所以無法做出最後的裁定。但是從和實驗的比較來看，重整化確實一個非常有效的手段，因為重整化以後的QED與實驗的符合程度是目前為止所有物理理論中最好的，因而我們沒理由也沒必要去懷疑重整化的正確性以及場論的正確性。
