定義
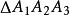 重心坐標
重心坐標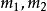 重心坐標
重心坐標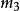 重心坐標
重心坐標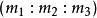 重心坐標
重心坐標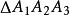 重心坐標
重心坐標設在平面上給出 .如果點X是這個三角形的頂點帶有質量 和 的質量中心,那么 稱做是點x關於 的重心坐標。
直線上的重心坐標
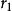 重心坐標
重心坐標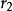 重心坐標
重心坐標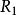 重心坐標
重心坐標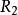 重心坐標
重心坐標 重心坐標
重心坐標 重心坐標
重心坐標我們首先在一條直線上定義點的重心坐標.設 和 是直線z上的兩個不同點 和 的向徑.那么, 上的任意一點P的向徑 可表示成
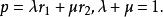 重心坐標
重心坐標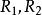 重心坐標
重心坐標而且這種表示法是唯一的.當點P線上段 上時,還需要下列條件
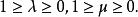 重心坐標
重心坐標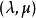 重心坐標
重心坐標這時,我們稱 為點P的重心坐標.
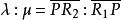 重心坐標
重心坐標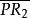 重心坐標
重心坐標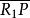 重心坐標
重心坐標重心坐標的幾何意義是明顯的: .這裡 和 表示相應線段的長.
平面上的重心坐標
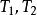 重心坐標
重心坐標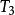 重心坐標
重心坐標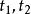 重心坐標
重心坐標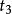 重心坐標
重心坐標 重心坐標
重心坐標設3點 和 構成三角形, 和 分別表示它們的向徑.對三角形所在平面上的任意一點P,可把它的向徑 表示為
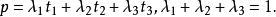 重心坐標
重心坐標 重心坐標
重心坐標這種表示方法是唯一的.事實上,設 還可表示成
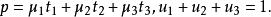 重心坐標
重心坐標 重心坐標
重心坐標將它與上述向徑 式相減,得到
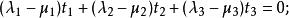 重心坐標
重心坐標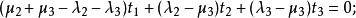 重心坐標
重心坐標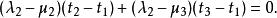 重心坐標
重心坐標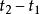 重心坐標
重心坐標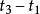 重心坐標
重心坐標因為與,是線性無關的,所以
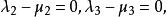 重心坐標
重心坐標即
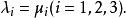 重心坐標
重心坐標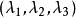 重心坐標
重心坐標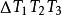 重心坐標
重心坐標稱是點P關於基的重心坐標.
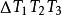 重心坐標
重心坐標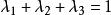 重心坐標
重心坐標如果點P在的內部或邊界上,則除了外,還成立
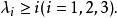 重心坐標
重心坐標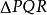 重心坐標
重心坐標重心坐標有下列幾何意義.用[PQR]表示有向的面積(有正負),則
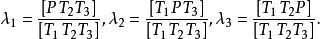 重心坐標
重心坐標 重心坐標
重心坐標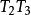 重心坐標
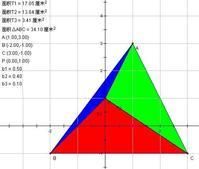
重心坐標為了證明這個結論,我們延長,使之與或其延長線相交於點Q,如圖1所示.根據直線上一點的重心
坐標的定義得知
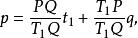 重心坐標
重心坐標而
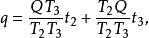 重心坐標
重心坐標所以
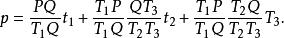 重心坐標
重心坐標由於重心坐標的唯一性,因此
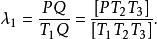 重心坐標
重心坐標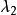 重心坐標
重心坐標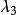 重心坐標
重心坐標由對稱性,同樣可以得出和的幾何意義。
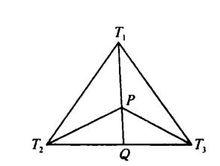 圖1
圖1與內心坐標的關係
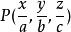 重心坐標
重心坐標若三角形ABC所在平面中一個點的重心坐標P(x,y,z),定義其內心坐標為,其中a、b、c為A、B、C對邊邊長。內心坐標是用P到三角形ABC三邊距離之比來刻畫P點的位置。三點共線的充要條件是內心坐標組成的三階行列式的值等於0。