命題
如果在兩個三角形中,有兩個邊和其中一邊的對角分別對應相等,那么這兩個三角形互為全等三角形。這個命題是假命題。但兩個三角形都分別為邊邊直角、邊邊鈍角、邊邊銳角時,這種情況成立。
證明
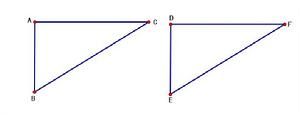
1.兩個三角形都是直角三角形的情況。
解:已知:∠A=∠D=90,AC=DF,AB=DE,∠B=∠E。
求證:△Abc≌△DEF
 1
1【AC=DF】
【AB=DE】
【∠A=∠D】
∴△ABC≌△DEF(SAS)
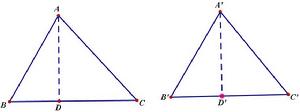
2.兩個三角形都是銳角三角形的情況。
解:已知:AB=A'B',AC=A'C',∠B=∠B'。
求證:△ABC≌△A'B'C'。
證明:過點A作垂線交BC於D。(另一幅圖同,不寫)
∵AD⊥BC,A'D'⊥B'C'
∴∠ADC=∠A'D'C'=90
 2
2【∠B=∠B'】
【∠ADB=∠A'D'B'】
【AB=A'B'】
∴△ABD≌△A'B'D'(AAS)
∴BD=B'D',AD=A'D'
∵AD⊥BC,A'D'⊥B'C'
∴∠ADC=∠A'D'C'=90
在Rt△ADC和Rt△A'D'C'中:
【AD=A'D'】
【AC=A'C'】
∴Rt△ADC≌Rt△A'D'C'(HL)
∴DC=D'C'
∴BD+B'D'=DC+D'C'
即BC=B'C'
在△ABC和△A'B'C'中:
【AB=A'B'】
【AC=A'C'】
【BC=B'C'】
∴△ABC≌△A'B'C'(SSS)
3.兩個三角形都是鈍角三角形的情況。
結論
如果兩個三角形均為直角三角形、銳角三角形、鈍角三角形,又符合有“在兩個三角形中,兩個邊和其中一邊的對角分別對應相等”的情況,那么這兩個三角形全等。
解:已知:AB=A'B',AC=A'C',∠B=∠B'。
求證:△ABC≌△A'B'C'。
證明:過點A作垂線交BC於D。(另一幅圖同,不寫)
∵AD⊥BC,A'D'⊥B'C'
∴∠ADC=∠A'D'C'=90 在△ABD和△A'B'D'中:
【∠B=∠B'】
【∠ADB=∠A'D'B'】
【AB=A'B'】
∴△ABD≌△A'B'D'(AAS)
∴BD=B'D',AD=A'D'
∵AD⊥BC,A'D'⊥B'C'
∴∠ADC=∠A'D'C'=90
在Rt△ADC和Rt△A'D'C'中:
【AD=A'D'】
【AC=A'C'】
∴Rt△ADC≌Rt△A'D'C'(HL)
∴DC=D'C'
∴BD+B'D'=DC+D'C'
即BC=B'C'
在△ABC和△A'B'C'中:
【AB=A'B'】
【AC=A'C'】
【BC=B'C'】
∴△ABC≌△A'B'C'(SSS)
