概念定義
A為角(angle) S為邊(side)
說理過程
把△ABC放到△A'B'C'上,使角A的頂點與角A'的頂點重合,由於角A=角A',因此可以使射線AB,AC分別落在射線A'B',C'A'上因為AB=A'B',AC=A'C',所以點B,C分別與點B',C'重合,這樣△ABC與△A'B'C'重合,即△ABC全等於△A'B'C'。
作用
作為全等三角形的判定方法,在生活中有廣泛套用。
重要題目
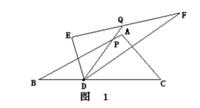 邊角邊
邊角邊如圖1,三角形DEF的頂點D在三角形ABC的邊BC上(不與B 、C 重合),且角BAC+角EDF=180度,AB=DF,AC=DE,點O 為EF 的中點。直線DO 交直線AB 於點P .
⑴猜想角BPD 與角FDB 的關係,並加以證明;(需詳細過程)
⑵當三角形DEF 繞點D 旋轉,其他條件不變,⑴中的結論是否始終成立?若成立,請你寫出真命題;若不成立請你在圖2中畫出相應的圖形,並給出正確的結論(不需要證明)
解:
證明:
(A.)分別作E,F關於D為對稱中心的對稱點G,H; 並連EG,FH,則
∵EH,FG互相平分於D點,∴E,F,H,G 構成平行四邊形,
∵QD為△FEG的中位線,∴QD//EG ,∴∠QDF=∠EGD
又∵ED=AC,DG=DF=AB,∠EDG=180°-∠EDF=∠BAC,
∴△GDE≌△BAC ∴∠EGD=∠ABC,
即∠QDF=∠ABC,
∠BDF=∠QDB+∠QDF=180°-∠ABC-∠BPD+∠ABC,
∴∠BDF+∠BPD=180°
(B.)在上述證明過程中,D在三角形ABC的邊BC上(不與B 、C 重合)
,只要DQ不與AB平行,∠BPD總是存在,現令DQ//AB時, ∠BPD=0°,此時
GF與BC重合,即B,D,F共線, 令∠BDF=180°.∴∠BDF+∠BPD=180°
因此,當三角形DEF 繞點D 旋轉,其他條件不變, ∠BDF+∠BPD=180°結論始終成立
