名詞介紹
 進制
進制進位制/位置計數法是一種記數方式,故亦稱 進位記數法/位值計數法,可以用有限的數字元號代表所有的數值。可使用數字元號的數目稱為基數(en:radix)或底數,基數為n,即可稱n進位制,簡稱n進制。現在最常用的是十進制,通常使用10個阿拉伯數字0-9進行記數。
對於任何一個數,我們可以用不同的進位制來表示。比如:十進數57(10),可以用二進制表示為111001(2),也可以用五進制表示為212(5),也可以用八進制表示為71(8)、用十六進制表示為39(16),它們所代表的數值都是一樣的。
進制一覽
十進制
人類天然選擇了十進制。
由於人類解剖學的特點,雙手共有十根手指,故在人類自發採用的進位制中,十進制是使用最為普遍的一種。成語“屈指可數”某種意義上來說描述了一個簡單計數的場景,而原始人類在需要計數的時候,首先想到的就是利用天然的算籌——手指來進行計數。
十進制編碼幾乎就是數值本身。
數值本身是一個數學上的抽象概念。經過長期的演化、融合、選擇、淘汰,系統簡便、功能全面的十進制計數法成為人類文化中主流的計數方法,經過基礎教育的訓練,大多數的人從小就掌握了十進制計數方法。盤中放了十個蘋果,通過數蘋果我們抽象出來“十”這一數值,它在我們的腦海中就以“10”這一十進制編碼的形式存放和顯示,而不是其它的形式。從這一角度來說,十進制編碼幾乎就是數值本身。
十進制的基數為10,數碼由0-9組成,計數規律逢十進一。
二進制
二進制有兩個特點:它由兩個數碼0,1組成,二進制數運算規律是逢二進一。
為區別於其它進制,二進制數的書寫通常在數的右下方註上基數2,或加後面加B表示,其中B是英文二進制Binary的首字母。
例如:二進制數10110011可以寫成(10110011),或寫成10110011B。對於十進制數可以不加標註,或加後綴D,其中D是英文十進制Decimal的首字母D。計算機領域我們之所以採用二進制進行計數,是因為二進制具有以下優點:
1) 二進制數中只有兩個數碼0和1,可用具有兩個不同穩定狀態的元器件來表示一位數碼。例如,電路中某一通路的電流的有無,某一節點電壓的高低,電晶體的導通和截止等。
2) 二進制數運算簡單,大大簡化了計算中運算部件的結構。
二進制數的加法和乘法基本運算法則各有四條,如下:
0+0=0,0+1=1,1+0=1,1+1=10
0×0=0,0×1=0,1×0=0,1×1=1
3)二進制天然兼容邏輯運算。
但是,二進制計數在日常使用上有個不便之處,就是位數往往很長,讀寫不便,如:把十進制的100000D寫成二進制就是11000011010100000B,所以計算機領域我們實際採用的是十六進制。二進制數轉換為十六進制數時,長度縮減為原先的約四分之一,把十進制的100000寫成八進制就是303240。十六進制的一個數位可代表二進制的四個數位。這樣,十進制的100000寫成十六進制就是186A0。
四進制
四進制是以4為基數的進位制,以 0、1、2 和 3 四個數字表示任何實數。 四進制與所有固定基數的計數系統有著很多共同的屬性,比如以標準的形式表示任何實數的能力(近乎獨特),以及表示有理數與無理數的特性。有關屬性的討論可參考十進制和二進制,下面是十進制0至15與四進制與二進制的互換。
| Qua (四進) | Bin (二進) | Dec (十進) |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 10 | 0100 | 4 |
| 11 | 0101 | 5 |
| 12 | 0110 | 6 |
| 13 | 0111 | 7 |
| 20 | 1000 | 8 |
| 21 | 1001 | 9 |
| 22 | 1010 | 10 |
| 23 | 1011 | 11 |
| 30 | 1100 | 12 |
| 31 | 1101 | 13 |
| 32 | 1110 | 14 |
| 33 | 1111 | 15 |
七進制
七進制是以7為基數的計數系統。使用數碼0-6。
七進制小數通常都是循環小數,除非分母是七的倍數。有些小數可以用有限個數字來表示,如:
| 十進制 | 七進制 (循環部分) |
| 1/2 | 1/2 = 0.3... |
| 1/3 | 1/3 = 0.2... |
| 1/4 | 1/4 = 0.15... |
| 1/5 | 1/5 = 0.1254... |
| 1/6 | 1/6 = 0.1... |
| 1/7 | 1/10 = 0.1 |
| 1/8 | 1/11 = 0.06... |
| 1/9 | 1/12 = 0.053... |
| 1/10 | 1/13 = 0.0462... |
| 1/12 | 1/15 = 0.04... |
| 1/14 | 1/20 = 0.03... |
| 1/15 | 1/21 = 0.0316... |
| 1/16 | 1/22 = 0.03... |
| 1/18 | 1/24 = 0.025... |
| 1/19 | 1/25 = 0.024... |
| 1/20 | 1/26 = 0.0231... |
| 1/21 | 1/30 = 0.02... |
| 1/24 | 1/33 = 0.02... |
| ... | ... |
| 1/49 | 1/100 = 0.01 |
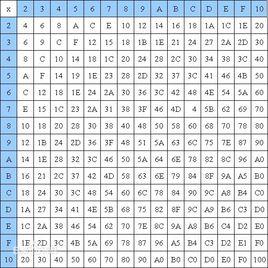
七進制的乘法表:
| - | 1 | 2 | 3 | 4 | 5 | 6 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 10 |
| 2 | 2 | 4 | 6 | 11 | 13 | 15 | 20 |
| 3 | 3 | 6 | 12 | 15 | 21 | 24 | 30 |
| 4 | 4 | 11 | 15 | 22 | 26 | 33 | 40 |
| 5 | 5 | 13 | 21 | 26 | 34 | 42 | 50 |
| 6 | 6 | 15 | 24 | 33 | 42 | 51 | 60 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 100 |
在七進制中:π = 3.0663651432... e = 2.5012410654...
加法運算舉例:1、131+245=406 2、406+666=1405 3、1405+3456=5164數制轉換舉例:1、十進制的131轉化成七進制數131(十)=18*7+5=(2*7+4)*7+5=2*7^2+4*7^1+5=245(七)2、七進制數245轉化成十進制數245(七)=2*7^2+4*7^1+5=2*49+4*7+5=98+28+5=131(十)
七進制的一個好處是,3.1 (22/7)是圓周率的一個很好的近似值。
八進制
由於二進制數據的基數R較小,所以二進制數據的書寫和閱讀不方便,為此,在小型機中引入了八進制。八進制的基數R=8=2^3,有數碼0、1、2、3、4、5、6、7,並且每個數碼正好對應三位二進制數,所以八進制能很好地反映二進制。八進制用下標8或數據後面加O表示 例如:二進制數據 ( 11 101 010 . 010 110 100 )2 對應八進制數據 (352.264)或352.264O。
十二進制
十二進制 長度單位一英尺等於12英寸,一先令等於12便士,就連足球比賽罰點球的英制長度也是12碼,不過這個12碼與十二進制並無關係,巧合而已。
十二進制來源:傳說是十個手指頭加兩隻腳。這是過去規定的,20世紀開始規定一打dozen為12個。
規定一打12個是一種12進制。
瑞典歷史上有一位有遠見的國王就說過,從日常套用的角度看,十二進制比十進制更方便。他生前曾構想過,在他管轄的範圍內取消十進制,而代之以十二進制。
直到2015年還能見到十二進制,比如鐘錶轉一圈12小時等等。
| 十進制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 十二進制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | M | N |
有時十進制中的10/11在十二進制中也用A/B表示。
十六進制
由於二進制數在使用中位數太長,不容易記憶,所以又提出了十六進制數。
十六進制數有兩個基本特點:它由十六個數碼:數字0~9加上字母A-F組成(它們分別表示十進制數10~15),十六進制數運算規律是逢十六進一,即基數R=16=2^4,通常在表示時用尾部標誌H或下標16以示區別,在c語言中用添加前綴0x以表示十六進制數。
例如:十六進制數4AC8可寫成(4AC8),或寫成4AC8H。
六十進制
古代人由於生產勞動的需要,要研究天文和曆法,就牽涉到時間和角度了。因為曆法需要的精確度較高,時間的單位小時,角度的單位度都嫌太大。必須進一步研究他們的小數。它們的小數都具有這樣的性質︰使1/2,1/3,1/4,1/5,1/6等都能成為它的整數倍。以1/60作為單位,就正好具有這個性質。譬如︰1/2等於30個1/60,1/3等於20個1/60,1/4等於15個1/60…這種小數的進位制在表示有些數時很方便。例如常遇到的1/3,在十進位制中是一個無限小數,但在這種進位制中就是一個有限小數。
位權概念
對於形式化的進制表示,我們可以從0開始,對數字的各個數位進行編號,即個位起往左依次為編號0,1,2,……;對稱的,從小數點後的數位則是-1,-2,……
進行進制轉換時,我們不妨設源進制(轉換前所用進制)的基為R1,目標進制(轉換後所用進制)的基為R2,原數值的表示按數位為AnA(n-1)……A2A1A0.A-1A-2……,R1在R2中的表示為R,則有(AnA(n-1)……A2A1A0.A-1A-2……)R1=(An*R^n+A(n-1)*R^(n-1)+……+A2*R^2+A1*R^1+A0*R^0+A-1*R^(-1)+A-2*R^(-2))R2
(由於此處不可選擇字型,說明如下:An,A2,A-1等符號中,n,2,-1等均應改為下標,而上標的冪次均用^作為前綴)
舉例:
一個十進制數110,其中百位上的1表示1個10^2,既100,十位的1表示1個10^1,即10,個位的0表示0個10^0,即0。
一個二進制數110,其中高位的1表示1個2^2,即4,低位的1表示1個2^1,即2,最低位的0表示0個2^0,即0。
一個十六進制數110,其中高位的1表示1個16^2,即256,低位的1表示1個16^1,即16,最低位的0表示0個16^0,即0。
可見,在數制中,各位數字所表示值的大小不僅與該數字本身的大小有關,還與該數字所在的位置有關,我們稱這關係為數的位權。
十進制數的位權是以10為底的冪,二進制數的位權是以2為底的冪,十六進制數的位權是以16為底的冪。數位由高向低,以降冪的方式排列。
進數轉換
1.二進制數、十六進制數轉換為十進制數(按權求和)
二進制數、十六進制數轉換為十進制數的規律是相同的。把二進制數(或十六進制數)按位權形式展開多項式和的形式,求其最後的和,就是其對應的十進制數——簡稱“按權求和”.
例如:把(1001.01)2 二進制計算。
解:(1001.01)2
=8*1+4*0+2*0+1*1+0*(1/2)+1*(1/4)
=8+0+0+1+0+0.25
=9.25
把(38A.11)16轉換為十進制數
解:(38A.11)16
=3×16的2次方+8×16的1次方+10×16的0次方+1×16的-1次方+1×16的-2次方
=768+128+10+0.0625+0.0039
=906.0664
2.十進制數轉換為二進制數,十六進制數(除2/16取余法)
整數轉換.一個十進制整數轉換為二進制整數通常採用除二取余法,即用2連續除十進制數,直到商為0,逆序排列餘數即可得到――簡稱除二取余法.
例:將25轉換為二進制數
解:25÷2=12 餘數1
12÷2=6 餘數0
6÷2=3 餘數0
3÷2=1 餘數1
1÷2=0 餘數1
所以25=(11001)2
同理,把十進制數轉換為十六進制數時,將基數2轉換成16就可以了.
例:將25轉換為十六進制數
解:25÷16=1 餘數9
1÷16=0 餘數1
所以25=(19)16
3.二進制數與十六進制數之間的轉換
由於4位二進制數恰好有16個組合狀態,即1位十六進制數與4位二進制數是一一對應的.所以,十六進制數與二進制數的轉換是十分簡單的.
(1)十六進制數轉換成二進制數,只要將每一位十六進制數用對應的4位二進制數替代即可――簡稱位分四位.
例:將(4AF8B)16轉換為二進制數.
解: 4 A F 8 B
0100 1010 1111 1000 1011
所以(4AF8B)16=(1001010111110001011)2
(2)二進制數轉換為十六進制數,分別向左,向右每四位一組,依次寫出每組4位二進制數所對應的十六進制數――簡稱四位合一位.
例:將二進制數(000111010110)2轉換為十六進制數.
解: 0001 1101 0110
1 D 6
所以(111010110)2=(1D6)16
轉換時注意最後一組不足4位時必須加0補齊4位
數制轉換的一般化
1)R進制轉換成十進制
任意R進制數據按權展開、相加即可得十進制數據。例如:N = 1101.0101B = 1*2^3+1*2^2+0*2^1+1*2^0+0*2^-1+1*2^-2+0*2^-3+1*2^-4 = 8+4+0+1+0+0.25+0+0.0625 = 13.3125
N = 5A.8H = 5*16^1+A*16^0+8*16^-1 = 80+10+0.5 = 90.5
2)十進制轉換R 進制
十進制數轉換成R 進制數,須將整數部分和小數部分分別轉換.
1.整數轉換——---除R 取余法 規則:(1)用R 去除給出的十進制數的整數部分,取其餘數作為轉換後的R 進制數據的整數部分最低位數字; (2)再用R去除所得的商,取其餘數作為轉換後的R 進制數據的高一位數字; (3)重複執行(2)操作,一直到商為0結束。例如:115 轉換成 Binary數據和Hexadecimal數據 (圖2-4) 所以 115 = 1110011 B = 73 H
2.小數轉換————---乘R 取整法 規則:(1)用R 去乘給出的十進制數的小數部分,取乘積的整數部分作為轉換後R 進制小數點後第一位數字; (2)再用R 去乘上一步乘積的小數部分,然後取新乘積的整數部分作為轉換後R 進制小數的低一位數字; (3)重複(2)操作,一直到乘積為0,或已得到要求精度數位為止。
3.小數轉換——整數退位法:舉例:0.321d轉成二進制,由於321不是5的倍數,用取余法、取整法可能要算很久,這時候我們可以採用整數退位法。原理如下:
n為轉成的二進制數的小數位數
(x)10=(y)2
(x)10*2^n=(y)2*2^n
D=(x)10*2^n:計算10進制數,取整
D→T轉成2進制數
(y)2=T/2^n=T*2^(-n),T退位,位數不足前端補零
舉例:
0.321轉成二進制數,保留7位
0.321*2^7=41.088,取整數41
41=32+8+1即100000+1000+1=101001
退位,因只有6位而要求保留7位,所以是0.0101001
用線上轉換工具校驗,正確
and、or、xor運算
所有進制的and(和)、or(或)、xor(異或)運算都要轉化為二進制進行運算,然後對齊位數,進行運算,具體的運算方法和普通的and、or、xor相同,如:1and1=1,1and0=0,0and0=0,1or1=1,1or0=1,0or0=0,1xor1=0,1xor0=1,0xor0=0。就是一般的二進制運算。
如:35(H)and5(O)=110101(B)and101(B)=101(B)=5(O)