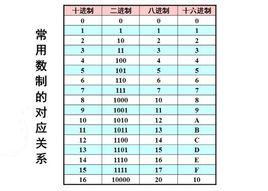
概念
以0x開始的數據表示16進制,計算機中每位的權為16,即(16進制)10 = (10進制)1×16
備註:這裡的0是數字0,不是字母O!
意義
編程中,我們常用的還是10進制……畢竟C/C++是高級語言。
比如:
int a = 100,b = 99;
不過,由於數據在計算機中的表示,最終以二進制的形式存在,所以有時候使用二進制,可以更直觀地解決問題。
但,二進制數太長了。比如int 類型占用4個位元組,32位。比如100,用int類型的二進制數表達將是:
0000 0000 0000 0000 0000 0000 0110 0100
面對這么長的數進行思考或操作,沒有人會喜歡。因此,C,C++ 沒有提供在代碼直接寫二進制數的方法。
用16進制或8進制可以解決這個問題。因為, 進制越大,數的表達長度也就越短。不過,為什麼偏偏是16或8進制,而不其它的,諸如9或20進制呢?
2、8、16,分別是2的1次方,3次方,4次方。這一點使得三種進制之間可以非常直接地互相轉換。8進制或16進制縮短了二進制數,但保持了二進制數的表達特點。在下面的關於進制轉換的課程中,你可以發現這一點。
相關換算
2進制,用兩個阿拉伯數字:0、1;
8進制,用八個阿拉伯數字:0、1、2、3、4、5、6、7;
10進制,用十個阿拉伯數字:0到9;
16進制,用十六個阿拉伯數字……等等,阿拉伯人或說是印度人,只發明了10個數字啊?
16進制就是逢16進1,但我們只有0~9這十個數字,所以我們 用A,B,C,D,E,F這六個字母來分別表示10,11,12,13,14,15。字母不區分大小寫。
十六進制數的第0位的權值為16的0次方,第1位的權值為16的1次方,第2位的權值為16的2次方……
所以,在第N(N從0開始)位上,如果是是數 X (X 大於等於0,並且X小於等於 15,即:F)表示的大小為 X * 16的N次方。
假設有一個十六進數 2AF5, 那么如何換算成10進制呢?
用豎式計算:
2AF5換算成10進制:
第0位: 5 * 16^0 = 5
第1位: F * 16^1 = 240
第2位: A * 16^2 = 2560
第3位: 2 * 16^3 = 8192 +
-------------------------------------
10997
直接計算就是:
5 * 16^0 + F * 16^1 + A * 16^2+2 * 16^3 = 10997
(別忘了,在上面的計算中,A表示10,而F表示15)
表達方法
如果不使用特殊的書寫形式,16進制數也會和10進制相混。隨便一個數:9876,就看不出它是16進制或10進制。
C,C++規定, 16進制數必須以 0x開頭。比如 0x1表示一個16進制數。而1則表示一個十進制。另外如:0xff,0xFF,0X102A,等等。其中的x也不區分大小寫。(注意:0x中的0是數字0,而不是字母O)
以下是一些用法示例:
int a = 0x100F;
int b = 0x70 + a;
至此,我們學完了所有進制:10 進制,8進制,16進制數的表達方式。最後一點很重要,C/C++中,10進制數有正負之分,比如12表示正12,而-12表示負12,;但 8進制和16進制只能用來表示無符號的正整數,如果你在代碼中里:-078,或者寫:-0xF2,C,C++並不把它當成一個負數。
使用
轉義符也可以接一個16進制數來表示一個字元。如在6.2.4小節中說的 '?' 字元,可以有以下表達方式:
'?' //直接輸入字元
'\77' //用八進制,此時可以省略開頭的0
'\0x3F' //用十六進制
同樣,這一小節只用於了解。除了空字元用八進制數 '\0' 表示以外,我們很少用後兩種方法表示一個字元。
互相轉換
二進制和十六進制的互相轉換比較重要。不過這二者的轉換卻不用計算,每個C,C++程式設計師都能做到看見二進制數,直接就能轉換為十六進制數,反之亦然。
我們也一樣,只要學完這一小節,就能做到。
首先我們來看一個二進制數:1111,它是多少呢?
你可能還要這樣計算:1 * 2 ^0+ 1 * 2^1 + 1 * 2^2+ 1 * 2^3 = 1 * 1 + 1 * 2 + 1 * 4 + 1 * 8 = 15。
然而,由於1111才4位,所以我們必須直接記住它每一位的權值,並且是從高位往低位記,:8、4、2、1。即,最高位的權值為2= 8,然後依次是 2 = 4,=2, 2 = 1。
記住8421,對於任意一個4位的二進制數,我們都可以很快算出它對應的10進制值。
下面列出四位二進制數 xxxx 所有可能的值(中間略過部分)
僅4位的2進制數 快速計算方法 十進制值 十六進值
1111 = 8 + 4 + 2 + 1 = 15 F
1110 = 8 + 4 + 2 + 0 = 14 E
1101 = 8 + 4 + 0 + 1 = 13 D
1100 = 8 + 4 + 0 + 0 = 12 C
1011 = 8 + 0 + 2 + 1 = 11 B
1010 = 8 + 0 + 2 + 0 = 10 A
1001 = 8 + 0 + 0 + 1 = 9 9
....
0001 = 0 + 0 + 0 + 1 = 1 1
0000 = 0 + 0 + 0 + 0 = 0 0
二進制數要轉換為十六進制,就是以4位一段,分別轉換為十六進制。
如(上行為二制數,下面為對應的十六進制):
1111 1101 , 1010 0101 , 1001 1011
F D , A 5 , 9 B
反過來,當我們看到 FD時,如何迅速將它轉換為二進制數呢?
先轉換F:
看到F,我們需知道它是15(可能你還不熟悉A~F這五個數),然後15如何用8421湊呢?應該是8 + 4 + 2 + 1,所以四位全為1 :1111。
接著轉換 D:
看到D,知道它是13,13如何用8421湊呢?應該是:8 + 4 + 1,即:1101。
所以,FD轉換為二進制數,為: 1111 1101
由於十六進制轉換成二進制相當直接,所以,我們需要將一個十進制數轉換成2進制數時,也可以先轉換成16進制,然後再轉換成2進制。
比如,十進制數 1234轉換成二制數,如果要一直除以2,直接得到2進制數,需要計算較多次數。所以我們可以先除以16,得到16進制數:
| 被除數 | 計算過程 | 商 | 餘數 |
| 1234 | 1234/16 | 77 | 2 |
| 77 | 77/16 | 4 | 13 (D) |
| 4 | 4/16 | 0 | 4 |
結果16進制為: 0x4D2
然後我們可直接寫出0x4D2的二進制形式:0100 1101 0010。
其中對映關係為:
0100 -- 4
1101 -- D
0010 -- 2
同樣,如果一個二進制數很長,我們需要將它轉換成10進制數時,除了前面學過的方法是,我們還可以先將這個二進制轉換成16進制,然後再轉換為10進制。
下面舉例一個int類型的二進制數:
01101101 11100101 10101111 00011011
我們按四位一組轉換為16進制: 6D E5 AF 1B