代數定義
由n個生成元生成, 且生成元滿足以下關係的群稱作辮群：
B_n=< x_1,x_2,...,x_{n-1}| x_ix_j=x_jx_i, x_ix_{i+1}x_i=x_{i+1}x_ix_{i+1}, |i-j|≥2 >
辮群中的元素稱作辮。
幾何解釋
考慮圓盤D, 設K是D中n個點的集合, u是D的邊界上一點. 考慮D到自身的微分同胚映射f:D-->D，並要求f(K)=K且f保持D邊界不變。這樣的f顯然誘導了基本群\pi_1(D-K,u)的自同構. 假設g是另一個滿足以上條件的微分同胚。 如果f和g誘導的基本群自同構一樣, 我們就說f和g是等價的.
所有滿足以上條件的微分同胚映射全體集合，在等價意義下構成的群稱作n條弦生成辮群, 其中的元素稱作辮。
辮群還可以用另一方式定義。 考慮平面上n個不同點組成的無序點組。 這樣的點組構成的集合--記作M--有自然的拓撲。 M的基本群就稱作n條弦生成辮群。 辮群中的的幾何直觀解釋相當於說：兩排點組之間連線n條弦(弦與弦之間無交點)， 如圖所示。
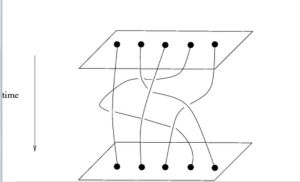辮群的幾何直觀圖形Artin有限實現定理
Artin的有限實現定理就是說， 辮群的代數定義與幾何定義是完全一致的。
這個結論的證明的困難之處在於如何說明辮群中的生成元的關係都來自於x_ix_j=x_jx_i以及x_ix_{i+1}x_i=x_{i+1}x_ix_{i+1}(稱為辮關係)。
純辮群
設B_n辮群, S_n是n元置換群. 由辮群的幾何定義容易看到以下滿同態
h_n:B_n--->S_n
該同態的核P_n=Ker h_n稱作純辮群。
利用Artin定理， 我們很容易寫出純半群的生成元.
正半扭辮
圖中的辮的幾何直觀圖形稱作（正）半扭辮。 這樣的半扭辮中可以挑選出一部分，作為辮群的生成元。
從直觀圖形上， 人們很容易驗證辮群的那些辮關係。
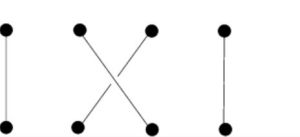正半扭辮