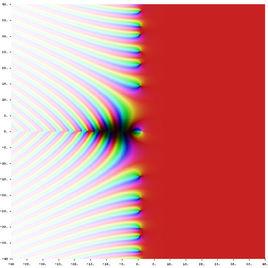
定義
以超越數為研究對象的數論分支之一。全體複數可分為兩大類:代數數和超越數。如一個複數是某個係數不全為零的整係數多項式的根,則稱此複數為代數數。不是代數數的複數,叫做超越數 。
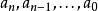 超越數論
超越數論 超越數論
超越數論超越數是代數數的相反,也即是說若是一個超越數,那么對於任何整數都符合:
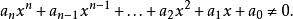 超越數論
超越數論(其中a≠0)
發展史
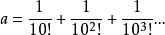 超越數論
超越數論歷史上第一個證明了超越數存在性的是法國數學家劉維爾(J.Liouville,1809~1882),他於1851年構造了一個數:這個無限小數後來被稱為“劉維爾數”。劉維爾成功地證明了這個數是一個超越數。在“劉維爾數”構造出來之後二十多年,數學家康托證明了:所有代數數的集合是可數的,即代數數的個數與自然數一樣多!在此基礎上,康托根據他的集合論中的另外一個結論——實數集是不可數的,得知複數集也是不可數的,因而進一步得到一個結論:必定存在不是代數數的複數,因此超越數必定存在!繼劉維爾之後,數學家們為了證明某些具體的數的超越性付出了種種努力:1873年,法國數學家埃爾米特(C.Hermite,1822~l901)證明了自然對數的底e=2.7182818……是超越數。1882年,德國數學數學家林德曼(Lindemann,1852~1939)證明了圓周率π=3.1415926……是超越數 。
劉維爾開創了對超越數的研究,他發現無理代數數的有理數逼近的精密性有一個限度,藉此他於1844年構造出歷史上第一批超越數。早在1844年以前的一個世紀裡,對無理數的研究已成為一個注意焦點。1744年,歐拉證明了自然對數的底e是無理數。1761年,朗伯證明了圓周率π是無理數。
1873年,埃爾米特證明了e是超越數,從而使超越數論進入一個新階段。1882年,林德曼推廣了埃爾米特的方法,證明了π是超越數,從而解決了古希臘的“化圓為方”問題。
19世紀超越數論的最高成就,是林德曼-外爾施特拉斯定理。
1900年,希爾伯特提出的23個問題中的第7問題是:如果是不等於0和1的代數數,是無理代數數,那么是否超越數希爾伯特曾預言,這個問題的解決將遲於黎曼猜想和費馬大定理。蓋爾豐德於1929年證明了:若是不等於零和1的代數數,是二次復代數數,則是超越數。庫茲明於1930年把這個結果推廣到是二次實代數數的情形。1934年,蓋爾豐德和施奈德獨立地對希爾伯特第7問題作出了肯定回答,此即所謂蓋爾豐德-施奈德定理。由此可知,若是正有理數,則常用對數lg不是有理數,便是超越數;更一般地,對非零代數數,,,,若ln,ln在上線性無關。
超越數論的最新發展使用著來自交換代數、代數幾何、多複變函數論、甚至上同調理論的方法,正處於活躍之時。
超越數的意義
證明某些數是超越數有著重大的意義,比如說π的超越性的證明就徹底地解決了古希臘三大作圖問題中的化圓為方問題,即化圓為方是不可能的。判斷某些給定的數是否超越數實在是太困難了,為了獲得上述結果,一個多世紀以來,數學家們付出了艱苦的勞動。即便如此,這個領域仍舊迷霧重重。比如說,現今仍然無法斷定像e+π和這樣的數到底是代數數還是超越數。
了解超越數
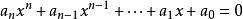 超越數論
超越數論 超越數論
超越數論實數中除代數數以外的數,亦即不滿足任一個整係數代數方程 (n為正整數, ≠0)的數。理論上證明超越數的存在並不難,而且可知超越數是大量的。但要構造一個超越數或論證某個數是超越數就極為困難。現今只有少量的數如π,e,等的超越性得到了證明,對其他一些有興趣的數的超越性的研究是數學家十分關注的事。
例子
超越數的例子包括:
錢珀瑙恩數
劉維爾數
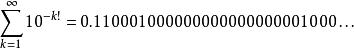 超越數論
超越數論它是第一個確認為超越數的數,是於1844年劉維爾發現的。
 超越數論
超越數論(參見:e)。
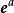 超越數論
超越數論 超越數論
超越數論,其中是除0以外的代數數。
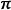 超越數論
超越數論 超越數論
超越數論林德曼-魏爾斯特拉斯定理,1882年,註:因是超越數而證明尺規作圖中的“化圓為方”的不可實現性。
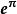 超越數論
超越數論(參見:e的π次方)
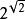 超越數論
超越數論 超越數論
超越數論 超越數論
超越數論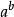 超越數論
超越數論更一般地,若為零和一以外的任何代數數及為無理代數數則必為超越數。這就是格爾豐德-施奈德定理。
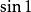 超越數論
超越數論(參見:正弦)
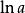 超越數論
超越數論 超越數論
超越數論(參見:自然對數),其中為一不等於1的正有理數。
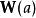 超越數論
超越數論 超越數論
超越數論(參見:朗伯W函式),其中為一正有理數。
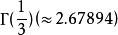 超越數論
超越數論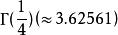 超越數論
超越數論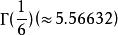 超越數論
超越數論,及(參見伽瑪函式)。
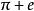 超越數論
超越數論所有超越數構成的集是一個不可數集。這暗示超越數遠多於代數數。可是,現今發現的超越數極少,甚至連是不是超越數也不知道,因為要證明一個數是超越數或代數數是十分困難的。
超越數的證明,給數學帶來了大的變革,解決了幾千年來數學上的難題——尺規作圖三大問題,即倍立方問題、三等分任意角問題和化圓為方問題。隨著超越數的發現,這三大問題被證明為不可能。