介紹
超圓法解數學物理問題的一種近似方法,是美國的W.普拉格和J.L.辛格於1947年在討論彈性靜力問題時提出的。辛格後來又把它推廣套用於一般數學物理邊值問題。實質上超圓法是一種函式空間方法,其特點是將泛函分析的解析概念形象化。用它能具體地給出問題精確解的上下界。超圓法屬於泛函分析的範疇,在用它處理實際問題時,須解決下面三個問題:①選擇什麼函式或函式集合來對應於函式空間的一個點或矢量;②確定函式空間中合適的數量積的定義,並給出函式空間的度量;③定義鬆弛問題,即定義函式空間中的全伴矢量、余矢量和齊次相伴矢量。
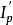 超圓法
超圓法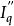 超圓法
超圓法用超圓法解彈性靜力問題時,所選擇的是實線性應力空間,空間中一個點P代表彈性體內一點的應力狀態 σ用函式集合σiy定義函式空間內一點P,它可用自原點O(σiy=0)到點P的位置矢量代表。其次,用應變能的兩倍定義函式空間中兩個矢量的數量積。再次,令S代表滿足彈性力學的平衡方程、應變協調方程和全部邊界條件的精確解;S'代表僅滿足平衡方程和應力邊界條件的基本應力解,即全伴矢量; S''代表僅滿足應變協調方程和位移邊界條件的基本位移解,即余矢量;( p=1,2,…, m)代表滿足自身平衡方程和零應力邊界條件的標準正交齊次應力矢量;( q=1,2,…, m)代表滿足應變協調方程和零位移邊界條件的標準正交齊次位移矢量。這樣,彈性靜力問題的解矢量S的端點就在圓心為C、半徑為R的超圓Г上,Г的方程為:
S=C+RJ, J ·J=1,
式中J是滿足下述正交條件的單位參數矢量(即J被限制在一個超平面上):
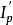 超圓法
超圓法J*=0( p=1,2,…, m),
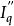 超圓法
超圓法J*=0( q=1,2,…, n);
而C和R由下列等式確定:
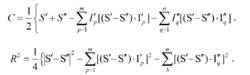 超圓法
超圓法Г上的矢量S滿足不等式:
| S|≤| S|≤| S|,
S和S分別為Г上離應力空間原點最近和最遠的點的矢量,它們可由下式確定:
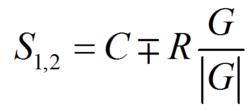 超圓法
超圓法式中矢量G為:
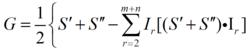 超圓法
超圓法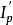 超圓法
超圓法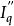 超圓法
超圓法式中 I( r=1,2,…, m+n)代表和的全部集合,它也是函式空間中的一組標準正交矢量。下圖在三維空間中表示出C、S、S和S之間的幾何關係。超圓法就是按上述過程找到S和S,並以它們作為真實應力矢量S的上、下界。