機率質量函式
注意這在所有實數上,包括那些X不可能等於的實數值上,都定義了 fX(x)。在那些X不可能等於的實數值上, fX(x)取值為0 ( x ∈ R\S,取Pr(X = x) 為0)。
離散隨機變數機率質量函式的不連續性決定了其累積分布函式也不連續。
例子
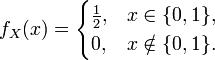 公式圖片
公式圖片假設X是拋硬幣的結果,反面取值為0,正面取值為1。則在狀態空間{0, 1}(這是一個Bernoulli隨機變數)中,X = x的機率是0.5,所以機率質量函式是:
機率質量函式可以定義在任何離散隨機變數上,包括常數分布, 二項分布 (包括Bernoulli分布), 反二項分布, Poisson分布, 幾何分布以及超幾何分布隨機變數上.
初始質量函式
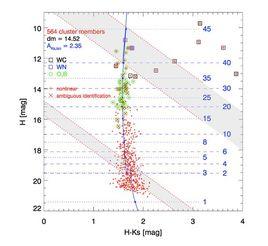
初始質量函式(縮寫為IMF)是同一個星族中單位體積內新形成的恆星的相對數目在質量上的分布,是恆星形成中的一個重要概念。初始質量函式首先是由薩爾彼得在1955年引入的[1],他將大於1倍太陽質量的初始質量函式寫為
ξ(M) = ξ0M − 2.35
其中M是恆星質量,ξ(M)是單位質量內新形成的恆星的數目,上式也稱為薩爾彼得方程。1979年Glenn E. Miller和John M. Scalo給出了1倍太陽質量以下的初始質量函式[2],稱為Miller-Scalo初始質量函式。
參考文獻
^ Salpeter, E.E., 1955, Astrophysical Journal, 121, 161. NASA ADS
^ Miller, G. E., Scalo, J. M., 1979, Astrophysical Journal Supplement Series, 41, 513. DOI:10.1086/190629 NASA ADS