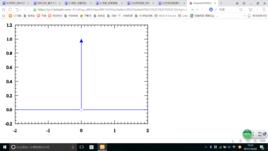
概念
物理學中常常要研究一個物理量在空間或時間中分布的密度,例如質量密度、電荷密度、每單位時間傳遞的動量(即力)等等,但是物理學中又常用到質點、點電荷、瞬時力等抽象模型,他們不是連續分布於空間或時間中,而是集中在空間中的某一點或者時間中的某一瞬時,那么它們的密度應該如何表示呢?
為了在數學上理想地表示出這種密度分布,引入了δ函式的概念。用數學表示為:
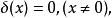 δ-函式
δ-函式 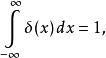 δ-函式
δ-函式 上述表達式不規定δ函式在0點的取值,是因為這個值無法嚴謹地表述出來,不能籠統的定義為正無窮,並且函式取值的“大小”是由第二個積分式決定的,因此只需限定取值為零的區域即可。如果函式不在0點取非零值,而在其他地方,可定義:
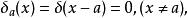 δ-函式
δ-函式 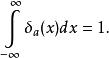 δ-函式
δ-函式 多維δ函式
定義
在多維空間中的δ函式定義如下:
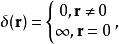 δ-函式
δ-函式 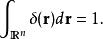 δ-函式
δ-函式 例如在三維空間中,三維δ函式可表示為三個一維δ函式乘積表示,在直角坐標系中,
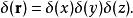 δ-函式
δ-函式 在極坐標系中,
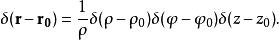 δ-函式
δ-函式 在球坐標系中,
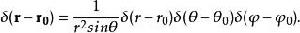 δ-函式
δ-函式 性質
多維的δ函式主要性質:
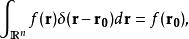 δ-函式
δ-函式 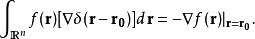 δ-函式
δ-函式 位矢的微分
δ函式可以表示如下:
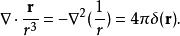 δ-函式
δ-函式 靜電場
密度表示
點電荷等抽象模型的密度分布可以表示為:
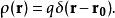 δ-函式
δ-函式 一組點電荷的電荷密度可以表示為:
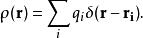 δ-函式
δ-函式 不僅可以用δ函式表示點電荷的密度分布,還可以表示圓柱、球殼上的電荷密度。例如,在電荷q均勻分布在半徑為a的球上,在球坐標系中其電荷密度為:
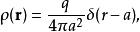 δ-函式
δ-函式 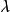 δ-函式
δ-函式 在半徑為b的圓柱上均勻分布的電荷單位長度的電荷為,在柱坐標系中其電荷密度為:
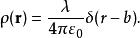 δ-函式
δ-函式 電場的方程
電學的高斯定理微分形式為:
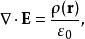 δ-函式
δ-函式 電場強度為:
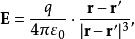 δ-函式
δ-函式 因此位矢的微分可以表示成:
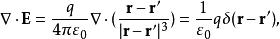 δ-函式
δ-函式 也可代入電荷密度的表達式直接得到。