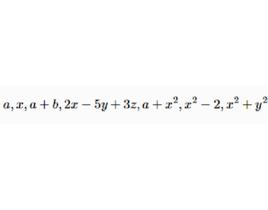質因數和質因式
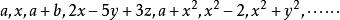 質因式
質因式在算術中我們把整數分成三類:單位1;質數,如2,3,5,7,11,等等;合數,如4,6,8,9,10,等等。 凡是只能被1和自己除盡的整數就都是 質數;換句話說,就是不含1和自己以外的因數的這種數就叫做質數。同樣,在代數中,不含1和自己以外的因式的這種式子就叫做 質式;例如:都是 質式 。
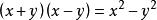 質因式
質因式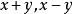 質因式
質因式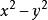 質因式
質因式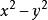 質因式
質因式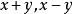 質因式
質因式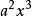 質因式
質因式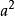 質因式
質因式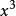 質因式
質因式 質因式
質因式 質因式
質因式如2,3,5,6,10,15都是30的因數,這裡面2,3,5是質數,它們就叫做30的 質因數。同樣,是的因式,也是的 質因式,因為都是質式;但如,和是它的因式,而不是質因式,和才是它的質因式。
這裡我們必須注意,在算術中我們有一定的法則來判定一個整數是不是質數,在代數中卻沒有一定的法則制定一個式子是不是質式 ,因此我們應當從演算中熟習一些質式的形式。
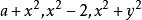 質因式
質因式註:①,作為質式是在初等代數中,就是在正負整數和分數範圍內說的,在高等代數中,除了這些數我們還得用到別的數,這三個式子也就可以不作為質式。
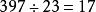 質因式
質因式 質因式
質因式②判定一個數是不是質數,我們可以用比它小的各質數依大小順序分別去除它,若除到商數比除數小還除不盡,這個數就是質數。例如,比397小的質數有2,3,5,7,11,13,17,19,23,……而用它們分別去除397都除不盡,並且余,商數17已經比除數23小,我們就判定397是個質數 。
單項式的因式
由於一個單項式是由一個數係數(注意數係數1常常略去不寫出來)和若干個字母或者式子連乘而構成的,所以只要將它所含的數係數和字母或式子分成幾組,每一組各構成一個單項式,這些單項式就都是原 單項式的因式。
 質因式
質因式 質因式
質因式 質因式
質因式例如,除含有數係數3外,還含2個和1個。若將它們分成兩組,就可以得因式
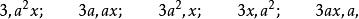 質因式
質因式若將它們分成三組,就可以得因式
 質因式
質因式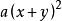 質因式
質因式又如,就可以有因式
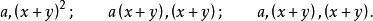 質因式
質因式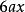 質因式
質因式當然,若單項式的數係數是一個合數,它也就可以分成若干個質因數,而用這些質因數的連乘積表示,在這種情形,又可以將數係數所含的質因數分組,例如的因式就可以是
 質因式
質因式 質因式
質因式