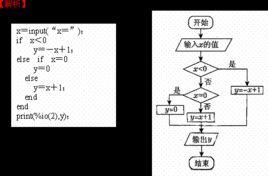
總述
在電腦程式設計語言中,用一定的賦值語句去實現變數的賦值,將確定的數值賦給變數的語句叫做賦值語句。賦值語句用來表明賦給某一個變數一個具體的確定值的語句叫做賦值語句。在算法語句中,賦值語句是最基本的語句。
賦值語句
將確定的數值賦給變數的語句叫做賦值語句。各程式設計語言有自己的賦值語句,賦值語句也有不同的類型。所賦“值”可以是數字,也可以是字元串和表達式。
注意很多語言都使用“等於號”(即“=”)來作為賦值號,所以可能和和平時的理解不同,在使用的時候應予以注意。
1、VB中的賦值格式
例如,給變數a賦值一個數為12,則格式為:a = 12 [注意:變數(即a)只能是一字母,而賦予的值可以是一個式子,當它是式子時,a的值就是這個式子的結果。
2、C語言中的賦值語句
如:
C語言規定,變數要先定義才能使用,也可以將定義和賦值在同一個語句中進行:
3、pascal語言中的賦值語句
可能略顯特殊,pascal語言要求在開頭定義變數,且賦值號為“:=”;
……
4、易語言中的賦值語句
易語言是中文編程的,賦值語法與大多數程式語言相似。
5、數學中的賦值
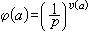 賦值
賦值實數(或複數)絕對值在任意域上的推廣。賦值這個概念最初是由J.屈爾沙克於1913年提出的。設 φ是定義在任意域 F上的一個取非負實數值的函式,並滿足以下三個條件:① φ( α)=0,若且唯若 α=0,並對某個 α∈ F有 φ( α)≠1;② φ( αb)= φ( α) φ( b);③ φ( α+ b)≤ φ( α)+ φ( b),J.屈爾沙克把這樣的 φ稱為 F上的一個賦值。按照通行的叫法,後改稱之為 F的絕對值。不久以後,A.奧斯特羅夫斯基引進了另一種絕對值 φ,它滿足上述的①和②,以及,並把這種 φ稱為非阿基米德絕對值,而把滿足①、②、③而不滿足④的那些 φ稱為阿基米德絕對值。實數域 R或複數域 C的通常絕對值就是它們的阿基米德絕對值。有絕對值 φ的域 F,記作( F, φ)。
6、完全域
藉助於F的絕對值φ,可以把分析學上的一些概念移植於F。設{αi}是F的一個序列。若對於每個實數ε>0,總有一個自然數n0,使得當m,n≥n0時,恆有φ(αm-αn)<ε,則稱{αi}是(F,φ)的一個φ柯西序列。若對於序列{αi},有α∈F,使得當n≥n0時恆有 φ(αn-α)<ε則稱{αi}是φ收斂的,而α稱為它的φ極限。若(F,φ)中每個φ柯西序列都是φ收斂的,則稱F關於φ是完全的,或者說(F,φ)是完全域(complete field)。實數域R或複數域C關於通常的絕對值是完全的,而K.亨澤爾的P進數域Qp則是一個非阿基米德絕對值的完全域。對這兩種域作統一的處理,正是發展賦值理論的一個主要出發點。F上所有形的級數,稱為F上關於文字X的形式冪級數。按照通常的加、乘運算,它們組成一個域,稱為F上的形式冪級數域,記作 F((x))。,以及ρ(0)=0,於是得到一個完全域(F((X)),φ)。
 賦值
賦值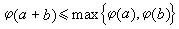 賦值
賦值當 φ是阿基米德絕對值時,有著名的奧斯特洛夫斯基定理:若 F關於阿基米德絕對值 φ是完全的,則 F連續同構於 R或 C。
7、賦值和賦值環
非阿基米德絕對值這個概念還可以作如下的推廣。設 Г是一個有序交換群,其運算為乘法,單位元素為1。設0是一個符號,它與Г的元素r,滿足r·0=0·r=0·0=0,以及0<r。若φ: F →Г∪{0}是個滿映射,滿足:①φ(α)=0若且唯若α=0;②φ(αb)=φ(α)·φ(b);,則稱φ是F的一個賦值.或者說F是有賦值φ的賦值域,記作(F,φ)。Г稱為φ的值群。當Г是正實數乘法群時,φ就是前面所說的非阿基米德絕對值。在賦值域(F,φ)中,子成一個環,稱為φ 的賦值環。F的子環A成為某個賦值的賦值環,若且唯若對於F的每個元素α,必有α∈A或者α_1∈A。
 賦值
賦值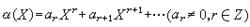 賦值
賦值從域F的一個子環A 到某個域K 的一個同態映射B,如果滿足:①對於α∈F-A,有α_1∈A以及α_1B=0;②B把 A的單位元素映射到 K的單位元素,那么B稱為 F的一個位。域的每個位,顯然給出一個賦值環;反之,從域的賦值環也不難作出域的一個位。因此,賦值、賦值環和位這三個概念密切相關。位還是代數幾何中的一個重要概念,早在R.戴德金和H.韋伯的經典著作中就有了它的雛型。賦值自W.克魯爾於20世紀30年代初提出以後,賦值理論廣泛套用於代數數論、類域論以及代數幾何等方面;到了60年代,它又與泛函分析有著日益增長的關聯。
8、賦值的階
設Г是賦值φ的值群,Δ是Г的一個子群。若對於Δ的每個元素δ,Г中所有滿足δ-1<у<δ的元素у也屬於Δ,則Δ稱為Г的一個孤立子群。{1}和Г都可以作為Г的孤立子群。以下設Г≠{1}。由於Г是有序的,Г中所有的孤立子群按包含關係成一個全序的集。除Г 本身外的所有孤立子群,按包含關係所成全序集的序型定義為Г的階。若φ的值群Г的階是m,就稱φ是m階賦值。因此,所謂一階賦值,就是指值群只有{1}為其真孤立子群的賦值。有序交換群的階為1,若且唯若它保序同構於某個由實數所成的乘法群。這個事實表明,一階賦值正是前面所定義的非阿基米德絕對值。
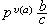 賦值
賦值9、離散賦值定義
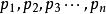 賦值
賦值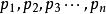 賦值
賦值設A為一個命題公式, 為出現在A中的所有的命題變項,給 指定一組真值,稱為對A的賦值或解釋,若指定的一組值使A值為真,則稱這組為A的成真賦值,若使A的值為假,則稱這組值為A的成假賦值 。
10、賦值的開拓
設(F,φ)是一個賦值域,K是F的一個擴域,若K有一個賦值ψ,使得對每個α∈F,都有ψ(α)=φ(α),則ψ稱為φ在K上的開拓。關於賦值開拓有存在性定理:F的賦值在F的任何一個擴域上都至少有一個開拓。
11、拓撲域
如果域F有一個拓撲τ,使得F的四則運算關於τ是連續的,那么F稱為關於τ的拓撲域,記作(F,τ)。庫爾雪克意義下的賦值域,是拓撲域的最早例子。 賦值理論也可以從拓撲代數的角度來研究,是基於下述事實。對於有絕對值φ 的域 F,所有形如{α∈F|φ(α)<ε}的子集構成零元素的一個基本鄰域族,從而生成F的一個域拓撲。在φ是F的賦值時,情形也相同。對拓撲域作系統的研究始於20世紀30年代初期D.von 丹齊克的工作。
12、局部緊域
任何拓撲域(F,τ)只能是連通的,或者完全不連通的。如果τ是F的一個局部緊拓撲,那么(F,τ)稱為局部緊域。離散拓撲也是一種局部緊拓撲。僅就非平凡的和非離散的情形而論,局部緊域有一些顯著的性質。首先,每個局部緊域 (F,τ)都有一個絕對值φ,使得由φ所生成的拓撲與τ相同。其次,還有定理:設(F,τ)是一個局部緊域。如果它是連通的,那么它連續同構於R或C(關於通常絕對值的拓撲);如果它是完全不連通的,那么它就連續同構於 p進數域Qp的一個有限擴域,或者某個有限域K上的形式冪級數域 K((x))的有限擴域。