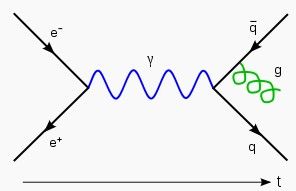
概述
兩個粒子的相互作用量由反應截面積所量化，其大小取決於它們的碰撞，該相互作用發生的機率尤其重要。 如果該相互作用的強度不太大（即是能夠用攝動理論解決），這反應截面積（或更準確來說是對應的時間演變運算元、分布函式或S矩陣）能夠用一系列的項（戴森級數）所表示，這些項能描述一段短時間所發生的故事，像以下的例子：
兩個具有一定相對速度的粒子在自由地移動（由兩條向著大致方向的線表示）
·它們遇到對方（兩線連於第一點──頂點）
·它們在同一路徑上漫步（兩線合二為一）
· 然後再度分開（第二個頂點）
· 但它們發覺自己的速度已變，而且再也不和之前一樣（兩線從最後的頂點向上──有時樣式會因應粒子所經歷的轉變而有所不同）
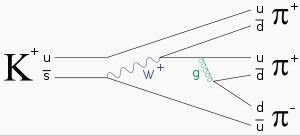本圖中，K介子（由一上夸克與反奇夸克組成）在弱相互作用下衰變成三個π介子，中間步驟有W玻色子及膠子參與。動機與歷史
粒子物理學中，計算散射反應截面積的難題簡化成加起所有可能存在的居間態振幅﹝每一個對應攝動理論又稱戴森級數的一個項﹞。用費曼圖表示這些狀態以，比了解當年冗長計算容易得多。從該系統的基礎拉格朗日量能夠得出費曼法則，費曼就是用該法則表明如何計算圖中的振幅。每一條內線對應虛粒子的分布函式；每一個線相遇頂點給出一個因子和來去的兩線，該因子能夠從相互作用項的拉格朗日量中得出，而線則約束了能量、動量和自鏇。費曼圖因此是出現在戴森級數每一個項的因子的符號寫法。
但是，作為攝動的展開式，費曼圖不能包涵非攝動效應。
除了它們在作為數學技巧的價值外，費曼圖為粒子的相互作用提供了深入的科學理解。粒子會在每一個可能的方式下相互作用：實際上，居間的虛粒子超越光速是允許的。（這是基於測不準原理，因深奧的理由而不違反相對論；事實上，超越光速對保留相對性時空的偶然性有幫助。）每一個終態的機率然後就從所有如此的機率中得出。這跟量子力學的功能積分表述有密切關係，該表述（路徑積分）也是由費曼發明的。
如此計算如果在缺少經驗的情況下使用，通常會得出圖的振幅為無窮大，這個答案在物理理論中是要不得的。問題在於粒子自身的相互作用被錯誤地忽視了。重整化的技巧（是由費曼、施溫格和朝永所開發的）彌補了這個效應並消除了麻煩的無窮大項。經過這樣的重整化後，用費曼圖做的計算通常能與實驗結果準確地吻合。
其他名稱
默里·蓋爾曼一直將費曼圖稱為斯蒂克爾堡圖(Stückelberg diagrams)，因為瑞士物理學家厄恩斯特·斯蒂克爾堡(Ernst Stückelberg)發明了一個相近的圖。歷史上他們也曾被叫成費曼-戴森圖或戴森圖。
例子
β衰變
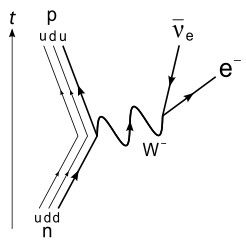β衰變的費曼圖
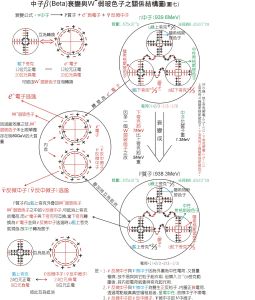β衰變-內部結構模型圖量子電動力學
在量子電動力學中，有兩個場標記，叫“電子”和“光子”。“電子”有一定方向而“光子”無固定方向。當中只有一種相互作用，用“γ”標記，其三度分別為“光子”、“電子”“頭”和“電子”“尾”。用途
費曼圖及路徑積分法亦被套用於統計力學中。
有關費圖及路徑積分的數學內容尚未完善，它還處於依賴物理直觀的階段。
量子場論微擾計算的一種圖示表示。是用方法的提出者的名字命名的.它為所考慮的物理過程提供了一個直觀圖像.對於給定的物理過程，它可以把微擾計算中要考慮的項都用圖表示出來.相反，按規則（稱費曼規則）根據這些圖可直接寫出要計算的微擾積分.它在微擾計算中起著指導作用.在相對論量子場論里，粒子可與外場作用，也可以通過虛規範粒子與其他粒子作用.費曼根據相互作用理論形式和微擾展開式的特點，給出了費曼規則：如何用圖把所考慮的具體物理過程和要計算的項表示出來；如何根據費曼圖把需要計算的積分寫出來.在量子電動力學裡，對於只有電子（－）、正`電子（＋）和光子（）的系統，相互作用可表示為K（）KG`H`oVHo（）（），可以看出，在同一點有三個場：電子場，正GVNV電子場和光子場，即一次相互作與這三個場相關聯.現在，費曼圖和費曼規則已被廣泛地套用在其他可重整的規範理論的微擾計算.電弱統一理論和量子色動力學在進行微擾計算時都套用費曼圖和費曼規則，使得物理圖像又清楚，計算又方便.
