定理定義
 貝亞蒂定理
貝亞蒂定理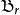 貝亞蒂定理
貝亞蒂定理定義一個正無理數的貝亞蒂列為
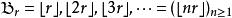 貝亞蒂定理
貝亞蒂定理 貝亞蒂定理
貝亞蒂定理,這裡的是取整函式。
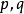 貝亞蒂定理
貝亞蒂定理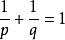 貝亞蒂定理
貝亞蒂定理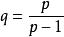 貝亞蒂定理
貝亞蒂定理若然有兩個正無理數且,(即)
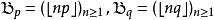 貝亞蒂定理
貝亞蒂定理則構成正整數集的一個分劃:
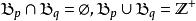 貝亞蒂定理
貝亞蒂定理套用例子
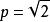 貝亞蒂定理
貝亞蒂定理取,那麽
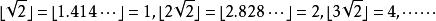 貝亞蒂定理
貝亞蒂定理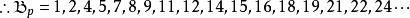 貝亞蒂定理
貝亞蒂定理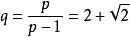 貝亞蒂定理
貝亞蒂定理然後
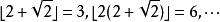 貝亞蒂定理
貝亞蒂定理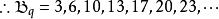 貝亞蒂定理
貝亞蒂定理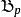 貝亞蒂定理
貝亞蒂定理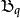 貝亞蒂定理
貝亞蒂定理可以看到,里的數不會在再出現,反之亦然。而且,每一個正整數都被這兩個數列無一遺漏地列舉了出來。
在數論中,貝亞蒂定理(英文:Beatty's theorem)指:若兩個正無理數的倒數之和是1,則任何正整數都可剛好以一種形式表示為不大於其中一個無理數的正整數倍的最大整數。 此定理由Sam Beatty在1926年發表。
 貝亞蒂定理
貝亞蒂定理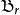 貝亞蒂定理
貝亞蒂定理定義一個正無理數的貝亞蒂列為
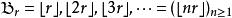 貝亞蒂定理
貝亞蒂定理 貝亞蒂定理
貝亞蒂定理,這裡的是取整函式。
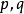 貝亞蒂定理
貝亞蒂定理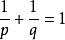 貝亞蒂定理
貝亞蒂定理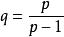 貝亞蒂定理
貝亞蒂定理若然有兩個正無理數且,(即)
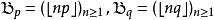 貝亞蒂定理
貝亞蒂定理則構成正整數集的一個分劃:
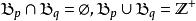 貝亞蒂定理
貝亞蒂定理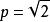 貝亞蒂定理
貝亞蒂定理取,那麽
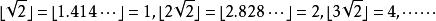 貝亞蒂定理
貝亞蒂定理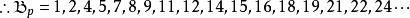 貝亞蒂定理
貝亞蒂定理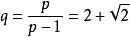 貝亞蒂定理
貝亞蒂定理然後
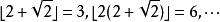 貝亞蒂定理
貝亞蒂定理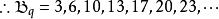 貝亞蒂定理
貝亞蒂定理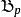 貝亞蒂定理
貝亞蒂定理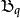 貝亞蒂定理
貝亞蒂定理可以看到,里的數不會在再出現,反之亦然。而且,每一個正整數都被這兩個數列無一遺漏地列舉了出來。
數學定理列表(按字母順序排列) 以下列出了許多數學定理,供查閱與引用。
在數論中,裴蜀定理是一個關於最大公約數(或最大公約式)的定理,裴蜀定理得名於法國數學家艾蒂安·裴蜀。 裴蜀定理說明了對任何整數 a、b和它們的最大公約數...
簡介 證明 n個整數間的裴蜀定理 任意主理想環上的情況 定理六旬的老父傑新娶了年輕美貌的妻子格勞麗亞,加上格勞麗亞和前夫所生的十歲...勞麗亞是老夫少妻的典範,傑的繼子曼尼少年老成,與傑的關係不似普通父子般...的方式理解哥倫比亞妻子格勞麗亞和繼子曼尼,不過事實表明文化差異並不容易...
劇情簡介 分集劇情 演職員表 角色介紹 幕後花絮六旬的老父傑新娶了年輕美貌的妻子格勞麗亞,加上格勞麗亞和前夫所生的十歲...勞麗亞是老夫少妻的典範,傑的繼子曼尼少年老成,與傑的關係不似普通父子般...的方式理解哥倫比亞妻子格勞麗亞和繼子曼尼,不過事實表明文化差異並不容易...
劇情簡介 分集劇情 演職員表 角色介紹 幕後花絮美國女攝影家。以珍藏照片和拍攝紀錄片聞名。早年在巴黎習藝期間曾當過曼·雷的助手,並結識了攝影家尤金·阿傑特。後自辦攝影室並拍攝了眾多名人的照片。阿傑特死...
簡介 生平 作品 評價亞冪等根(subidempotent radical)是一個特殊的根性質。指滿足下述條件的根性質R:R是遺傳的;每個R根環都是冪等環。在環結構定理中,通...
概念 環 環論 冪等電腦史話(新版)《電腦史話》● 1、 計算機始祖 ● 36、 蘋果穿雨衣 ● 2、 第一抹曙光 ● 37...
)。2004年:麥可·阿蒂亞(愛丁堡大學)與艾沙道爾·辛格(麻省理工...方程解的存在性與光滑性• 7貝赫和斯維訥通-戴爾猜想公布年月:2000年... Griggs Thompson)和法國法蘭西學院教授雅克·蒂茨...
數學研究 數學獎 國外著名數學家 華人數學家 部分數學家簡介,順手捎帶地證明了費馬大定理、哥德巴赫猜想,並用這種方法研究物理、化學和生物學等學科”。 證明費馬大定理蔣春暄自1973年開始研究費馬大定理。在此...大定理。 但其所著研究論文在投稿過程中常遇權威阻礙。早在1978年...
人物簡介 學術研究 學界爭議 發表作品