概念
亞冪等根(subidempotent radical)是一個特殊的根性質。指滿足下述條件的根性質R:R是遺傳的;每個R根環都是冪等環。在環結構定理中,通常捨棄環的冪零性而適當保留其冪等性。亞冪等根則是與傳統根完全不同的另一類根性質,它的出現不再是為了研究環的結構,而是根理論本身的需要,是公理化根性質中一種重要的類型。
環
環是對並與差運算封閉的集類,測度論中重要概念之一。設F是Ω上的一個非空集類。如果它對集的並及差運算封閉,即對任何A,B∈F,都有A∪B∈F,A\B∈F,則稱F為Ω上的環。例如,若F是由實直線R上任意有限個左開右閉的有限區間的並集:
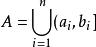 亞冪等根
亞冪等根的全體構成的集類,則F是R上的一個環。環也是對於交與對稱差運算封閉的集類,並按這兩種運算成為布爾環。要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。
環論
一個環是一個集合R,其中有兩個合成運算,叫作加法和乘法,對有序對a,b,a,b∈R,其結果分別用a+b和ab表示,這兩個合成法則滿足:(1)a+b及ab屬於R(閉合);(2)a + b=b + a(交換律);(3) (a+b) + c=a+ (b + c)(結合律);(4)在R中有一個元0叫零元,對R中任意a,適合a + 0 = 0 +a;(5)對R中任意元a,在R中有一個a的負元—a,適合a+ (—a)=0;(6)(ab)c= a(bc);(7)a(b + c)=ab+ac,(b+c)a=ba+ca(分配律),滿足以上條件的代數系即叫環,環論研究的就是具有這些性質的代數系。環論概括了數學各分支中很多基本的特例,如它包括整數環、有理數環、實數環、複數環和各種不同的函式和矩陣環等。環是現代代數中重要概念,其理論和方法在數學許多分支中都有套用。
冪等
一個代數系統中,滿足方程x =x的元素x,稱為冪等元素。當A為集合,“·”為“並”,由於A ≡A·A=A,因此,A為冪等元素。對於矩陣的乘法運算,單位矩陣及矩陣等,都是冪等元素。
