三角形
三角形是由同一平面內不在同一直線上的三條線段‘首尾’順次連線所組成的封閉圖形,在數學、建築學有套用。
常見的三角形按邊分有普通三角形(三條邊都不相等),等腰三角(腰與底不等的等腰三角形、腰與底相等的等腰三角形即等邊三角形);按角分有直角三角形、銳角三角形、鈍角三角形等,其中銳角三角形和鈍角三角形統稱斜三角形。
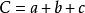 角邊角公理
角邊角公理若一個三角形的三邊分別為a、b、c,則周長 。
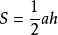 角邊角公理
角邊角公理面積公式為: (面積=底×高÷2。其中,a是三角形的底,h是底所對應的高)注釋:三邊均可為底,應理解為:三邊與之對應的高的積的一半是三角形的面積。這是面積法求線段長度的基礎。
全等三角形
簡介
經過翻轉、平移後,能夠完全重合的兩個三角形叫做全等三角形, 而該兩個三角形的三條邊及三個角都對應相等。全等三角形指兩個全等的三角形,它們的三條邊及三個角都對應相等。全等三角形是幾何中全等之一。根據全等轉換,兩個全等三角形經過平移、鏇轉、翻折後,仍舊全等。正常來說,驗證兩個全等三角形一般用邊邊邊(SSS)、邊角邊(SAS)、角邊角(ASA)、角角邊(AAS)、和直角三角形的斜邊,直角邊(HL)來判定。
性質
1.全等三角形的對應角相等。
2.全等三角形的對應邊相等。
3. 能夠完全重合的頂點叫對應頂點。
4.全等三角形的對應邊上的高對應相等。
5.全等三角形的對應角的角平分線相等。
6.全等三角形的對應邊上的中線相等。
7.全等三角形面積和周長相等。
8.全等三角形的對應角的三角函式值相等。
相關教學
 角邊角公理
角邊角公理對於角邊角公理的教學過程王嶸分了三個部分:公理的引入,公理的明確,公理的鞏固.與教材不同的是,我用一個生活中的實例設計問題情景引入公理.這就是問題一:有一塊三角形玻璃碎成如圖所示的兩塊,如果要將其復原,是不是兩塊都要帶去?
面對這樣的問題學生有了興趣而且議論紛紛,答案不一在此時教師應提出問題二:只帶一塊就行,帶哪一塊呢?還是隨便哪一塊都可以?此問題目的一給學生指明方向“一塊即可”;目的二將問題深入一層“帶哪塊去”。這時學生的思維進入活躍狀態,討論也更有針對性,他們或許對答案的選擇只是一種感覺“行或不行”。於是教師就要引導學生,指導學生尋求正確的答案。通過畫圖演示即可一目了然。
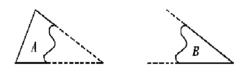 角邊角公理
角邊角公理走到這裡,可能學生認為問題一已得到圓滿地解決。就在這個點上,提出問題三:為什麼帶A可行,B不可行?這就涉及到了問題的本質,也要求學生思維跳躍性地思考。當他們處在欲言不能的狀態時,給予提示:“一個三角形六個元素,三條邊三個內角,帶A去帶去了三角形的幾個元素,帶B去帶去了三角形的幾個元素?哪幾個?學生通過觀察比較就會容易地得出答案。問問學生“恢復後的三角形和原三角形全等,那全等的條件是不是就是帶去的元素呢?至此學生就可以粗略地概括出角邊角的公理。
在以上的過程中非常值得注意的有兩點:1,教師的問題要提得恰時恰點,就在學生思維深入的轉折點上,如此才能發揮好的作用。2,對於學生,在這個過程中他們的思維經歷了“觀察—比較—分析—歸納—猜想”的路線.但這並沒結束,因為在數學中,猜想需要驗證才能說其正確與否,而這也是學生容易忽視的一點。因此在其後的公理明確中教師的任務有兩點:一是完善學生對公理的粗略概括,二是和學生一起做實驗,根據三角形全等定義對公理進行驗證。
概念
角邊角公理(ASA):兩個三角形對應的兩角及其夾邊相等,兩個三角形全等。
證明方法
對任意△ABC,畫一個△A'B'C',使A'B'=AB,∠A'=∠A,∠B'= ∠B:
1. 作A'B'=AB;
2.在A'B'的同旁作∠DA'B'=∠A,∠EB'A'=∠B,A'D,B'E交C.
即得所求。
舉例
 角邊角公理
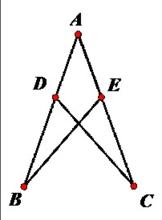
角邊角公理舉例:如下圖,AB=AC,∠B=∠C,求證△ABE≌△ACD.
證明:在△ABE與△ACD中∠A=∠A,AB=AC,∠B=∠C.
∴△ABE≌△ACD.(ASA)