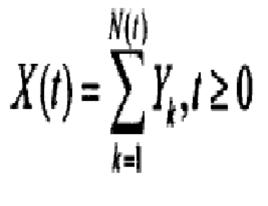基本概念
複合泊松過程(compound Poisson process)一類隨機過程。是由對泊松過程的每一點賦予一獨立同分布的隨機變數而得的隨機過程.對於隨機過程{X(t),t≥0}如果對任意t≥0,它能表為
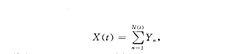 複合泊松過程
複合泊松過程其中{N(t),t≥0}是一泊松過程,而{Y,n=1,2,... }是一族獨立同分布的隨機變數,並且過程{N(t),t≥0}與序列{Y}是相互獨立的,則將它稱為複合泊松過程。
複合泊松過程可以看做是在泊松過程的點附上標值(用隨機變數Y表示)而得,因而是一類特殊的標值點過程.另一方面,複合泊松過程也可看做是一類特殊的濾過泊松過程,這時回響函式ω(t,τ,u)=Y(參見“標值點過程”和“濾過泊松過程”)。
計數過程
泊松過程是計數過程中最重要的類型之一,所以要了解泊松過程和複合泊松過程就要先了解計數過程,下文為計數過程的介紹。
稱隨機過程{N(t), t ≥0}為計數過程,若N(t)表示到時刻,為止已發生的“事件A”的總數,且N(t)滿足下列條件:
(1)N(t)≥0;
(2 ) N(t)取正整數值;
(3)若s<t,則N{s} ≤ N(t);
(4)若s<t,則N{t)一N(s)等於區間((s, t]中發生事件“事件A”的次數。
如果計數過程N(t)在不相重疊的時間間隔內,事件A發生的次數是相互獨立的,即若t1 < t2 < t3 < t4,則在(t1 , t2]內事件A發生的次數N(t2) - N(t1)與在(t3,t4]內事件A發生的次數N(t4) - N(t3 )相互獨立,此時計數過程N(t)是獨立增量過程。
若計數過程N(t)在(t,t+s]內(s>0),事件A發生的次數N(t + s)一N(t)僅與時間差s有關,則計數過程N(t)是平穩增量過程。
泊松過程(Poisson過程)
泊松過程是複合泊松過程的基礎,所以要了解複合泊松過程就要先了解泊松過程,下文是泊松過程的介紹。
Poisson過程是一種在實際中常被使用的計數隨機過程,它所描述的是考慮特定現象的發生次數隨時間變化的規律.如果計算在某一段時間內出現的隨機點的數目,這個數目也是隨機的,它隨著這段時間的延伸而不斷變化,則稱這個變化的過程為伴隨著隨機點過程的計數過程。
Poisson過程是一類特殊的計數過程,有很強的實際背景.如果一個隨機過程具有時間(或空間)上的均勻性(即時齊性),未來的變化與過去的變化沒有關係(即獨立增量性),並且具有普通性,則該隨機過程就是Poisson過程。
稱去非負整數的隨機過程{N(t), t ≥0}為強度(或速率)為λ的Poisson過程,如果滿足:
(1) N(0)=0;
(2) N(t)為平穩獨立增量過程;
(3)對任意的0≤s<t,增量N(t)一N(s)服從參數為λ(t一s)的Poisson分布.
設{N(t),t ≥0}為滿足上述三個條件的計數過程,則{N(t), t ≥0}是強度為λt的Poisson過程。
複合泊松過程
稱計數過程{N(t),t≥0}為具有參數λ>0的泊松過程,若它滿足下列條件:
(1)X(0)=0;
( 2) X (t)是獨立增量過程;
(3)在任一長度為t的區間中,事件A發生的次數服從參數為通的泊松分
布,即對任意的s,t≥ 0,有
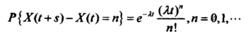 複合泊松過程
複合泊松過程注意,從條件(3)中知道泊松過程為平穩增量過程且E(X(t))=λt。
設{N(t), t ≥0}是服從參數為λ的泊松過程,{Yk,k=1,2,……}是一獨立同分布的隨機變數,且與{N(t), t ≥0}獨立,令
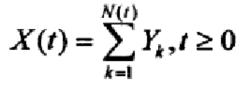 複合泊松過程
複合泊松過程則稱{x(t),t ≥0}為複合泊松過程。