基本介紹
在離散隨機過程中，計數過程在可靠性工程中運用很廣泛，可以用於描述失效、完全修複數等。 泊松過程(Poisson process)是最簡單的計數過程，但是泊松過程在可靠性的套用中扮演著很特殊的角色，一個經典的例子就是鈾衰變。核材料中的放射性粒子對特定目標的撞擊就是強度固定的泊松過程。 更新 過程也是一個著名的計數過程。更新過程被描述為一個事件的序列，事件的間隔時間為獨立同分布的隨機變數。在可靠性理論中，這種數學模型用來描述在時間間隔中事件的發生次數。
對於非負且取值為整數的隨機過程N(t)，如果N(t)表示時間間隔[0，t]內事件發生的總數，並滿足如下兩條特性，則N(t)為 計數過程：
(1)若t<t，則N(t)≤N(t)；
(2)若t<t，則N(t)-N(t)為時間間隔[t，t]間事件發生的總數。
例如，如果N(t)表示在t時刻之前進入一家飯店的人數，那么N(t)就是計數過程，只要有人進入飯店事件就會發生。
泊松過程
定義
泊松過程是最重要的計數過程之一。
計數過程定義1 滿足以下條件的計數過程N(t)被稱作強度為 的泊松過程：
(1)失效過程N(t)有平穩獨立增量。
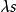計數過程(2)在任意時間間隔s內，失效數量服從均值為 的泊松分布，也就是說
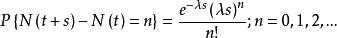計數過程(3)初始條件為N(0)=0。
計數過程這一模型也叫做 齊次泊松過程，這也暗示了故障率 不由時間t決定。也就是說，在時問間隔(t，t+s]中的失效數並不由當前時刻t決定，而是由時間間隔s唯一確定。如果一個計數過程在不相交的時問間隔中的事件數是相互獨立的，便說它擁有獨立增量。
具有獨立增量的隨機過程的自協方差函式為
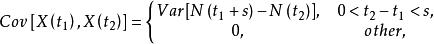計數過程其中
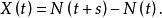計數過程如果X(t)服從泊松分布，那么泊松分布的方差為
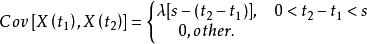計數過程這一結果表明泊松增量過程是協方差平穩的。接下來將給出泊松過程的幾條性質。
性質
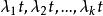計數過程
計數過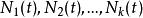程
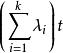計數過程性質1 均值分別為 的獨立泊松過程 的和也是一個泊松過程，其均值為 。換句話說，獨立的泊松過程的和也是泊松過程，且該泊松過程的均值為各獨立泊松過程的均值之和。
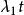計數過程
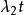計數過程性質2 均值分別為 和 的獨立泊松過程N(t)和N(t)的差不是泊松過程。它的機率質量函式為
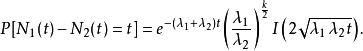計數過程
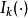計數過程其中， 為k階修正貝塞爾函式(Handbook 1980)。
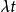計數過程
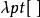計數過程性質3 如果對均值為 的泊松過程N(t)進行過濾，使得不完全計入每一個發生的事件．則該過程以恆定的機率p被計數。這樣，該過程就變為了均值為 的泊松過程。
性質4 令N(t)為泊松過程，Y為一組獨立同分布的隨機變數，同時也關於N(t)獨立，則將可以用以下方式表示的隨機過程X(t)稱為複合泊松過程：
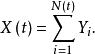計數過程更新過程
更新過程是更一般情況下的泊松過程，該過程的到達間隔時間或失效間隔時間不一定服從指數分布。為了方便，將事件的發生稱為一次更新，將到達間隔時間稱為 更新周期(renewal period)，將等待時間稱為更新時間(renewal time)。
定義2 計數過程N(t)表示時間間隔(0，t]之間事件發生的總次數，若失效間隔時問是獨立相同分布的隨機變數，則稱N(t)為更新過程。
在時間t之前恰好發生n次失效的機率為
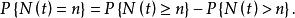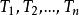計數過程
計數過程需要注意的是，失效間隔時間為 ，因此發生n個失效的時刻W為
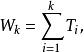計數過程並且
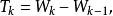計數過程因此
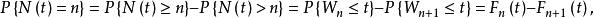計數過程其中，F(t)為第n次失效時間的累積分布函式，n=0，l，2，…。
