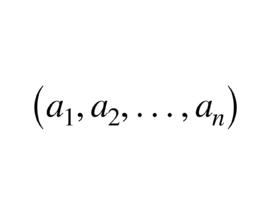定義
行向量的轉置是一個列向量,反之亦然。
所有的行向量的集合形成一個向量空間,它是所有列向量集合的對偶空間。
符號
為簡化書寫、方便排版起見,有時會以加上轉置符號 T的行向量表示列向量。
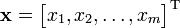 圖1.行向量的轉置
圖1.行向量的轉置為進一步化簡,習慣上會把行向量和列向量都寫成 行的形式。不過行向量的元素是用空格或逗號隔開,列向量則用分號隔開。例如,假設 x是一個行向量,那么 x和 x的轉置就可以如下方式表示。
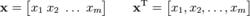 圖2.行向量的表示
圖2.行向量的表示矩陣
[matrix]
 行向量
行向量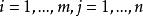 行向量
行向量設 F 是一個環或域,F 中的 mn 個元素 , ,排成一個表:
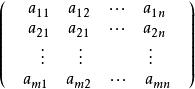 行向量
行向量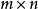 行向量
行向量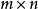 行向量
行向量 行向量
行向量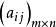 行向量
行向量稱為 F 上的一個 m 行 n 列矩陣,或 階矩陣,簡稱 矩陣, 稱為矩陣的元素(entry of matrix),或更明確地,矩陣的 (i,j) 元素。上述矩陣亦常記作 或字母 A 。
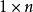 行向量
行向量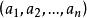 行向量
行向量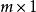 行向量
行向量 行向量
行向量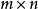 行向量
行向量矩陣 稱為 F 上的一個 n 元行向量,對應地, 矩陣 稱為 F 上的一個 m 元列向量(column vector),一個 矩陣的各行構成的 m 個行向量稱為矩陣的行向量,各列構成的 n 個列向量稱為矩陣的列向量。
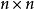 行向量
行向量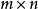 行向量
行向量矩陣稱為 n 階方陣(square matrix),而稱一般的 矩陣為長方陣(rectangular matrix)。
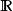 行向量
行向量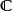 行向量
行向量最常見的是 F 取實數域 或複數域 ,這時的矩陣分別為實矩陣(real matrix)或復矩陣(complex matrix)。