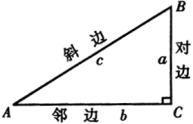
定義
弦值是在直角三角形中,對邊的長比上斜邊的長的值。 任意銳角的正弦值等於它的餘角的餘弦值,任意銳角的餘弦值等於它的餘角的正弦值。
sin30°=1╱2 sin45°=√2╱2 sin60°=√3╱2 sin90°=1 sin180°=0 sin0°=0 sin270°=-1
三角函式表
特殊三角函式值
| θ → | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| 函式值→ | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sinθ | 0 | 1/2 | √2/2 | √3/2 | 1 | 0 | -1 | 0 |
| cosθ | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
| tanθ | 0 | √3/3 | 1 | √3 | / | 0 | / | 0 |
| cotθ | / | √3 | 1 | √3/3 | 0 | / | 0 | / |
註:在上面的表格中,例如:√3/2 指的是(√3)/2
sin30°=1╱2 sin45°=√2╱2 sin60°=√3╱2 sin90°=1 sin180°=0 sin0°=0 sin270°=-1
其他公式
三角函式 是必背的
Sin2A=2sinA·cosA
cos2A=cos^2A-sin^2A=1-2sin^2A=2cos^2A-1
tan2A=(2tanA)/(1-tan^2A)
同角三角函式的基本關係式
倒數關係: 商的關係: 平方關係:
tanα ·cotα=1
sinα ·cscα=1
cosα ·secα=1 sinα/cosα=tanα=secα/cscα
cosα/sinα=cotα=cscα/secα sin2α+cos2α=1
1+tan2α=sec2α
1+cot2α=csc2α
誘導公式
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα
(其中k∈Z)
萬能公式
兩角和與差的三角函式公式萬能公式
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
tanα+tanβ
tan(α+β)=——————
1-tanα ·tanβ
tanα-tanβ
tan(α-β)=——————
1+tanα ·tanβ
2tan(α/2)
sinα=——————
1+tan2(α/2)
1-tan2(α/2)
cosα=——————
1+tan2(α/2)
2tan(α/2)
tanα=——————
1-tan2(α/2)
半角的正弦、餘弦和正切公式 三角函式的降冪公式
二倍角的正弦、餘弦和正切公式 三倍角的正弦、餘弦和正切公式
sin2α=2sinαcosα
cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α
2tanα
tan2α=—————
1-tan2α
sin3α=3sinα-4sin3α
cos3α=4cos3α-3cosα
3tanα-tan3α
tan3α=——————
1-3tan2α
三角函式的和差化積公式三角函式的積化和差公式
α+β α-β
sinα+sinβ=2sin—--·cos—-—
2 2
α+β α-β
sinα-sinβ=2cos—--·sin—-—
2 2
α+β α-β
cosα+cosβ=2cos—--·cos—-—
2 2
α+β α-β
cosα-cosβ=-2sin—--·sin—-—
2 2 1
sinα ·cosβ=-[sin(α+β)+sin(α-β)]
2
1
cosα ·sinβ=-[sin(α+β)-sin(α-β)]
2
1
cosα ·cosβ=-[cos(α+β)+cos(α-β)]
2
1
sinα ·sinβ=- -[cos(α+β)-cos(α-β)]
2
化asinα ±bcosα為一個角的一個三角函式的形式(輔助角的三角函式的公式)
常用函式數值
α=0°(0)
sinα=0
cosα=1
tαnα=0
cotα→∞
secα=1
cscα→∞α=15°(π/12)
sinα=(√6-√2)/4
cosα=(√6+√2)/4
tαnα=2-√3
cotα=2+√3
secα=√6-√2
cscα=√6+√2
α=22.5°(π/8)
sinα=√(2-√2)/2
cosα=√(2+√2)/2
tαnα=√2-1
cotα=√2+1
secα=√(4-2√2)
cscα=√(4+2√2)α=30°(π/6)
sinα=1/2
cosα=√3/2
tαnα=√3/3
cotα=√3
secα=2√3/3
cscα=2α=45°(π/4)
sinα=√2/2
cosα=√2/2
tαnα=1
cotα=1
secα=√2
cscα=√2α=60°(π/3)
sinα=√3/2
cosα=1/2
tαnα=√3
cotα=√3/3
secα=2
cscα=2√3/3α=67.5°(3π/8)
sinα=√(2+√2)/2
cosα=√(2-√2)/2
tαnα=√2+1
cotα=√2-1
secα=√(4+2√2)
cscα=√(4-2√2)α=75°(5π/12)
sinα=(√6+√2)/4
cosα=(√6-√2)/4
tαnα=2+√3
cotα=2-√3
secα=√6+√2
cscα=√6-√2α=90°(π/2)
sinα=1
cosα=0
tαnα→∞
cotα=0
secα→∞
cscα=1α=180°(π)
sinα=0
cosα=-1
tαnα=0
cotα→∞
secα=-1
cscα→∞α=270°(3π/2)
sinα=-1
cosα=0
tαnα→∞
cotα=0
secα→∞
cscα=-1α=360°(2π)
sinα=0
cosα=1
tαnα=0
cotα→∞
secα=1
cscα→∞