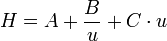范德姆特方程

范德姆特方程（英語：Van Deemter equation）在色譜學中是綜合考慮了分離過程中引起峰展寬的物理因素、動力學因素和熱力學因素後得到的單位柱長的總峰展寬與流動相流速的關係式。一般來說，影響峰展寬的因素包括多路徑效應，擴散（徑向的和軸向的）與固定相和流動相間的傳質阻力。液相色譜中的流動相流速常取出口的流速，即體積流量與柱橫截面積之比。對於填充柱來說，通常取出口橫截面積為柱橫截面積的0.6倍。另一種方法是用柱長與死時間的比。如果流動相是氣相，還要進行溫度與壓強的校正。通常用理論塔板高度來表示色譜分離過程中的峰展寬。范德姆特方程呈雙曲形函式的形式，表明流動相的流速存在一個最優值，在該點柱效最高。范第姆特方程是將色譜速率理論運用於色譜洗脫過程的分析中得到的。。

簡單形式

范德姆特方程最常用的形式如下式所示，該式直觀地反映了流動相流速對於分離的影響。

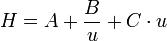范德姆特方程

式中A, B, C為常數， u表示流動相的流速。

A項反映的是被分析物在填充柱中可能採取不同的路徑，因而經過的路程也不一樣長，引起色譜峰的展寬，這就是“多路徑效應”。在毛細管開管柱中不存在多路徑效應，這一項為零。

B/ u 表示的是因為色譜柱各部分存在濃差而引起的縱向擴散帶來的峰展寬。

C u表示達到固定相與流動相的平衡之後由於在固定相與流動相傳質存在著阻力引起的峰展寬。

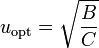范德姆特方程

微分後可得到最佳流速為

完整形式

范德姆特方程的完整形式如下：

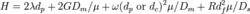范德姆特方程

式中：

H 為理論塔板高度

λ 是一個與柱內填料粒度均一性與填充狀態有關的常數

dp 為填料的粒徑

G, ω 和 R 為常數

Dm 是被分析物在流動相中的分子擴散係數

dc 是毛細管的直徑

df 是固定相的膜厚度

Ds 是被分析物在固定相中的分子擴散係數