脈衝函式的定義
 脈衝函式
脈衝函式 脈衝函式
脈衝函式脈衝函式是英國物理學家狄拉克(Dirac)在20世紀20年代引人的,用於描述瞬間或空間幾何點上的物理量。例如,瞬時的衝擊力、脈衝電流或電壓等急速變化的物理量,以及質點的質量分布、點電荷的電量分布等在空間或時間上高度集中的物理量。 脈衝函式也稱函式。若在一維空間中,自變數為時間 t 的函式,滿足下述兩個條件:
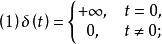 脈衝函式
脈衝函式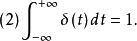 脈衝函式
脈衝函式 脈衝函式
脈衝函式 脈衝函式
脈衝函式 脈衝函式
脈衝函式 脈衝函式
脈衝函式把滿足上述兩個條件的函式稱為函式,記作。函式是一種廣義函式,也可以擴展到多維空間中,它的確切意義應該在積分運算下理解:其積分曲線高度為“無限高”,而寬度為“無限窄”,曲線下的面積等於1。因此,函式有下述關係式
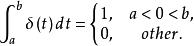 脈衝函式
脈衝函式 脈衝函式
脈衝函式 脈衝函式
脈衝函式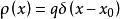 脈衝函式
脈衝函式 脈衝函式
脈衝函式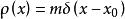 脈衝函式
脈衝函式有了函式的定義,就可以把處於x 軸上點處、電量為q的點電荷,用線電荷密度函式來描述;把一維坐標點處的質點m,用質量線密度函式來描述;...... 。
δ函式的性質
下面我們直接給出δ函式的幾個基本性質 。
性質1 (篩選性質)設f(t)是定義在實數域上的有界函式,且在t處連續,則
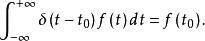 脈衝函式
脈衝函式特別地,當t=0時,則有
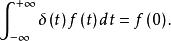 脈衝函式
脈衝函式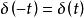 脈衝函式
脈衝函式性質2 δ函式為偶函式,即。
性質3 設u(t)為單位階躍函式,即
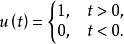 脈衝函式
脈衝函式則有
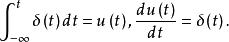 脈衝函式
脈衝函式脈衝函式的傅氏變換
根據δ函式的篩選性質,易知δ函式的傅氏變換為
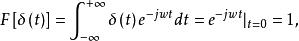 脈衝函式
脈衝函式即δ(t)與F(w)=1構成一傅氏變換對,按傅氏積分公式有
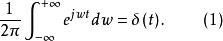 脈衝函式
脈衝函式這是一個關於δ函式的重要公式。
公式(1)並不是常規意義下的積分問題,故稱δ(t)的傅氏變換為一種廣義傅氏變換。在工程技術中,有許多函式並不滿足絕對可積條件,如符號函式、單位階躍函式以及正、餘弦函式等,然而利用δ函式的傅氏變換就可以求出它們的傅氏變換了,從這個角度也可以看出引進δ函式的重要性 。
脈衝函式的拉氏變換
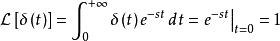 脈衝函式
脈衝函式脈衝函式的拉氏變換為。