表達式
奇異函式通常是指下列函式族:
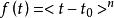 奇異函式
奇異函式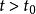 奇異函式
奇異函式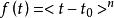 奇異函式
奇異函式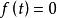 奇異函式
奇異函式當n>0或n=0時,且 時, ,否則 ;
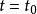 奇異函式
奇異函式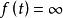 奇異函式
奇異函式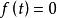 奇異函式
奇異函式當n<0時,若 ,則 ,否則 。
 奇異函式相關書籍
奇異函式相關書籍上式中< >一般稱為麥考利(W.H.Macauley)括弧。
物理學中套用
在物理學中,經常要用處理一些包含某種無窮大的量以及不連續函式的微分等問題,因而引入一種“非正規函式”。這種函式最初於二十世紀三十年代,由著名物理學家狄拉克在量子力學研究中引入和定義。後來被命名為“狄里克δ函式”,簡稱為“δ函式”。五十年代法國數學家施瓦茨在深入研究δ函式性質的基礎上,創立了分布論(亦即廣義函式論)。他從理論上嚴格證實了不僅可以使用δ函式,而且還可以δ函式及其各階導數,從而使δ函式理論趨於完整和嚴密。
常用奇異函式
在物理學中,人們習慣的將包括δ函式的各階導數,亥維賽(O.Heaviside)階躍函式(簡稱為階躍函式)及其各階積分的函式族稱為奇異函式。在物理學中,奇異函式套用最多的是階躍函式u(t)和δ函式δ(t)。
套用舉例
用奇異函式表示某些理想化了的物理模型
1.用奇異函式表示某些理想化了的物理模型
(1)力學中,集中量和分布量是經常遇到的兩種物理模型。如集中質量和分布質量,瞬時作用力和持續力等等。集中量和分布量的差異,給使用基於連續函式的傳統解法帶來了限制,因而在傳統的力學中,當遇到因集中量造成的不連續時,往往將對一個完整的問題的論述與表達進行分割和支離式的處理。實際上集中量與分布量可以用統一的方法來處理,所用的數學工具就是奇異函式。
(2)電路分析中,階躍函式是常用函式。當要表示一分段表示的信號時,利用階躍函式則一目了然。例如,可用階躍函式表示理想化了的開關接通信號源的情況。當信號為脈衝形式,利用階躍函式則使表達式變得簡單。
2.利用奇異函式解決起始點跳變值的確定問題
3.在信號分析中,視奇異函式為單元函式,可把任一函式分解為奇異函式的和,此時用該分解求線性非時變系統的零狀態回響。
材料力學套用
在材料力學中,一般是用截面法及積分法來求解梁彎曲時的內力及變形。此法對於載荷在梁長度上連續變化時比較方便,但當樑上出現不連續載荷時,如一個樑上同時作用多個集中力、集中力偶及分布力時,則必須分段寫出不同組的剪力和彎矩方程,常常導致很繁瑣的結果。例如,在求解梁的變形時,當樑上外力情況複雜時,將梁分成n段,對於彎矩M(x)在不同區段內的表達式分別列出n個撓曲線微分方程;然後逐段分別積分兩次,得到2n個積分常數,再由邊界條件及連續條件求得。如果採用奇異函式,則可使某些問題的演算大為簡化。由於奇異函式所表達出不連續性,那么,作為軸向位置函式的載荷集度(每單位長度的力)就能以一個方程的形式寫出,直接積分就得到整個梁的剪力方程,而剪力方程的積分就得到整個梁的彎矩方程。這樣,可根據一個方程直接觀察到整個梁的內力情況。如果對彎矩方程再積分兩次,則可得到一個方程表示整個梁的撓曲線,這時僅有兩個積分常數需滿足支坐邊界條件 。
套用舉例
用奇異函式求解梁彎曲變形的問題。但在用奇異函式解該類題時應注意以下幾點:
(1)奇異函式本身是不連續,而梁的各種狀態的最終結果也仍然是不連續的;
(2)必須將坐標原點置於所研究梁的一端;
(3)須假想地將均布載荷k和線性分布載荷q(x)沿x軸正向延續至另一端,同時還要假想地加上與延續載荷的集度大小相等而方向相反的分布載荷,以保持原載荷作用不變;
(4)注意線性分布荷載q(x)的絕對值沿x軸的正負方向。
用奇異函式求解超靜定梁的問題
在材料力學中,可以通過直接積分求解超靜定梁。但當所受外力較為複雜時,此法演算較為繁瑣,使用奇異函式可使得演算過程大大簡化,且提高計算的準確性,另外一方面有利於計算機的編程。
1.用奇異函式求解梁彎曲變形的問題。但在用奇異函式解該類題時應注意以下幾點:
(1)奇異函式本身是不連續,而梁的各種狀態的最終結果也仍然是不連續的;
(2)必須將坐標原點置於所研究梁的一端;
(3)須假想地將均布載荷k和線性分布載荷q(x)沿x軸正向延續至另一端,同時還要假想地加上與延續載荷的集度大小相等而方向相反的分布載荷,以保持原載荷作用不變;
(4)注意線性分布荷載q(x)的絕對值沿x軸的正負方向。
2.用奇異函式求解超靜定梁的問題
在材料力學中,可以通過直接積分求解超靜定梁。但當所受外力較為複雜時,此法演算較為繁瑣,使用奇異函式可使得演算過程大大簡化,且提高計算的準確性,另外一方面有利於計算機的編程。

