定義
普通函式
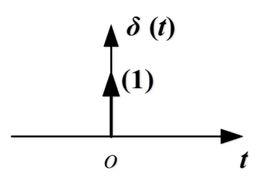
衝激函式的定義為:
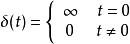 衝激函式
衝激函式單位衝擊函式
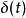 衝激函式
衝激函式通常,單位衝激函式
滿足: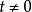 衝激函式
衝激函式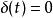 衝激函式
衝激函式(1)當 時,
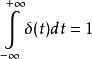 衝激函式
衝激函式(2)
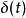 衝激函式
衝激函式 衝激函式
衝激函式單位衝激函式 又稱Dirac函式或者 函式。
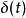 衝激函式
衝激函式註:單位衝激函式 並不是經典意義下的函式,而是一個廣義函式(或者奇異函式),它不能用通常意義下的“值的對應關係”來理解和使用,而是通過它的性質來使用。
廣義函式
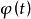 衝激函式
衝激函式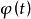 衝激函式
衝激函式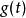 衝激函式
衝激函式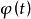 衝激函式
衝激函式 衝激函式
衝激函式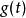 衝激函式
衝激函式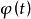 衝激函式
衝激函式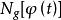 衝激函式
衝激函式選擇一類性能良好的函式 ,稱為檢驗函式 (它相當於定義域),一個廣義函式 對檢驗函式空間中的每個函式 賦予一個數值 的映射,該數與廣義函式 和檢驗函式 有關,記作 。廣義函式可寫為
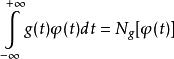 衝激函式
衝激函式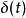 衝激函式
衝激函式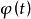 衝激函式
衝激函式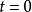 衝激函式
衝激函式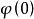 衝激函式
衝激函式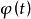 衝激函式
衝激函式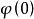 衝激函式
衝激函式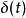 衝激函式
衝激函式衝擊函式 與檢驗函式的作用效果是從 中篩選出它在 時刻的函式值 ,這常稱為衝擊函式的取樣性質(或篩選性質)。簡言之,能從檢驗函式 中篩選出函式值 的廣義函式就稱為衝擊函式 。
性質
篩選性質
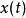 衝激函式
衝激函式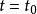 衝激函式
衝激函式如果信號 是一個在 處連續的普通函式,則有
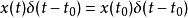 衝激函式
衝激函式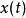 衝激函式
衝激函式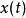 衝激函式
衝激函式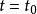 衝激函式
衝激函式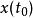 衝激函式
衝激函式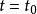 衝激函式
衝激函式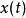 衝激函式
衝激函式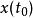 衝激函式
衝激函式上式表明,信號 與衝激函式相乘,篩選出連續時間信號 在 時的函式值 ,可以理解為衝激函式在 時刻對函式 的一瞬間的作用,其值是衝激函式和 相乘的結果,瞬間趨於無窮大 。
取樣性質
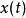 衝激函式
衝激函式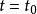 衝激函式
衝激函式如果信號 是一個在 處連續的普通函式,則有
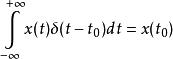 衝激函式
衝激函式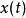 衝激函式
衝激函式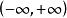 衝激函式
衝激函式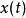 衝激函式
衝激函式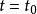 衝激函式
衝激函式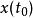 衝激函式
衝激函式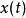 衝激函式
衝激函式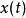 衝激函式
衝激函式 衝激函式
衝激函式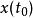 衝激函式
衝激函式衝激信號的取樣特性表明,一個連續時間信號 與衝激函式相乘,並在時間域 上積分,其結果為信號 在 時的函式值 。該式可以理解為衝激函式作用於函式 ,趨於穩態時最終作用的結果,即得到信號 在 時刻的值 。
導數性質
衝激函式的導數性質如下:
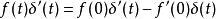 衝激函式
衝激函式其證明如下:
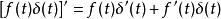 衝激函式
衝激函式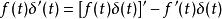 衝激函式
衝激函式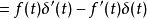 衝激函式
衝激函式尺度變換
衝激函式的尺度變換性質如下:
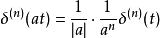 衝激函式
衝激函式其推論明如下:
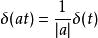 衝激函式
衝激函式(1)
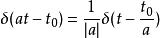 衝激函式
衝激函式(2)
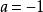 衝激函式
衝激函式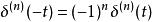 衝激函式
衝激函式(3) 當 時,
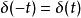 衝激函式
衝激函式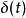 衝激函式
衝激函式(4) ,為偶函式
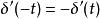 衝激函式
衝激函式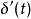 衝激函式
衝激函式(5) ,為奇函式
套用
衝激函式可用於信號處理,通過衝激函式來表示複雜的信號,可以簡化對複雜信號的一些特性的研究。衝激函式及其延時衝激函式的線性組合來表示或逼近,再利用系統的迭加原理,可以通過簡單的信號如單位衝激函式的頻譜,以及頻域特性來討論比較複雜信號的頻譜。從而減少計算複雜信號頻譜的難度 。