介紹
定義
系統是指確定的物理系統。例如飛機的自動駕駛系統、鍋爐的水位調節系統等,它們都是完成預定的任務由一些物理部件組合起來的一個集合體。控制系統就是使用控制手段所實現的物理系統。
按照對系統的輸入、輸出關係,一個系統可以分為線性系統或非線性系統。如果一個系統的輸入、輸出滿足疊加原理,該系統稱為線性系統,否則為非線性系統。疊加原理包括疊加性及齊次性。例如,系統輸入u,輸出y的關係為y=Hu,如滿足疊加原理:
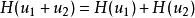 線性控制系統
線性控制系統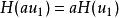 線性控制系統
線性控制系統其中u、u為任意兩輸入,a為任意實數。H是某一運算元或函式,它按照系統的輸入u唯一規定系統的輸出y。
類別
線性系統又分為時變系統和時不變系統兩類。如果系統的動態特性只與控制過程的時間間隔有關,而與具體的初始時刻和終止時刻無關,則該系統稱為時不變系統,又稱定常系統;如果系統的動態特性與控制系統的初始時刻及終止時刻有關,則該系統稱為時變系統,也稱非定常系統。
研究意義
研究線性系統理論的重要性在於:線性系統理論是現代控制理論中最基礎部分,也是最成熟的部分,它有完整的理論和設計、計算方法;線性系統理論在套用中起著較大的作用,大多數在正常運行範圍內工作的系統,均能用線性模型來描述;線性系統理論是研究非線性系統理論的基礎。
控制理論發展
在控制理論的發展過程中,依據對控制系統描述的數學方法不同而形成兩大類:經典控制理論及現代控制理論。經典控制理論是通過傳遞函式來表達系統的輸入—輸出關係的,主要的分析和綜合方法是:頻率回響法及根軌跡法,並且對單輸入—單輸出線性定常系統的分析和綜合是有效的。該理論有兩個局限性:第一,它只能描述單輸入—單輸出定常系統,難於處理多輸入—多輸出系統;第二,它只能表現系統輸入—輸出關係,而對系統內部結構不能提供任何信息,難以揭示系統更深刻的特性。客觀上,現代控制系統要求有一種完善的控制理論,計算機技術的進步又為控制理論的發展創造了條件,於是產生了一種描述系統的新的數學方法——狀態空間法。狀態空間法是建立在狀態變數概念上的,稱為現代控制理論。
現代控制理論與經典控制理論比較,它適用範圍廣,可用於單輸入—單輸出系統或多輸入—多輸出系統,線性或非線性系統,時不變系統或時變系統。現代控制理論可以設計出最優控制規律,使系統的性能指標最佳。它是時域分析方法,對控制過程是直接的,也可以考慮任意初始條件。
現代控制理論從50年代中、後期開始發展,目前已形成了若干分支,其中主要有線性系統理論、最優控制理論、最佳估計理論、系統辨識、自適應控制及大系統理論等。
就線性系統理論來說,由於採用的數學工具和採用的系統描述的不同,又分成若干平行分支,如線性系統的狀態空間法、線性系統的幾何理論、線性系統的代數理論等。狀態空間法是線性理論中一個最重要和影響最廣的分支。
數學描述
研究線性系統理論,首先要建立能反映實際物理系統特性的數學模型。由於所要解決的問題不同,所用的分析方法不同,描述同一系統的數學表達式也不相同。介紹描述控制系統的兩種數學模型,即輸入—輸出描述和狀態變數描述。通過等價變換,可改變系統動態方程的形式。
系統的輸入—輸出描述
系統的輸入—輸出描述給出了系統的輸入和輸出的關係。
一、線性時變系統
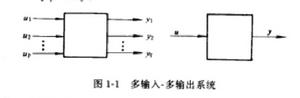 多輸入—多輸出系統
多輸入—多輸出系統設有多輸入—多輸出控制系統,如圖所示。該系統有p個輸入端,q個輸出端。
若系統的輸入端和輸出端均為1,即p=q=1,該系統稱為單變數系統,否則稱為多變數系統。
系統的輸入—輸出描述給出了系統的輸入與輸出之間的數學關係式,依據系統的輸入與輸出來推導這種描述時,無須知道系統內部結構。這種情況下,可把系統看作是一個"黑箱"。可以向黑箱施加各種類型的輸入並測量相應的輸出,從輸入,輸出數據中找出反映系統重要特性的規律。
利用脈衝函式的概念,容易求得系統的輸入—輸出關係。如圖所示的脈動函式方程
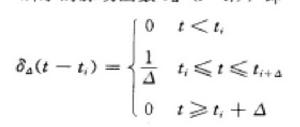 脈衝函式方程
脈衝函式方程t為某一特定時刻。當Δ趨於零時,δ(t-t)的極限δ(t-t)≌limδ(t-t) 稱為脈衝函式,或稱Diracδ函式,簡稱δ函式。δ函式有以下性質:
(1)對於任何正的小數ε,有
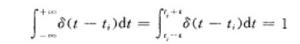 線性控制系統
線性控制系統(2)對在t連續的任何函式f(t),有
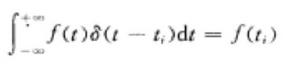 線性控制系統
線性控制系統設單變數系統的輸入—輸出關係為y=Hu,用脈衝函式近似輸入Hu,如圖所示,輸入“可閘一系列的脈動函式來近似,當Δ趨於零時,即
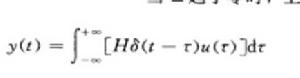 線性控制系統
線性控制系統上式表明,系統的輸出回響可以用脈衝回響函式和輸入的卷積表示。
若系統是具有p個輸入和q個輸出的多輸入—多輸出系統,則式(1—1)可相應地推廣為
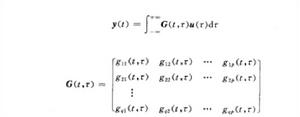 線性控制系統
線性控制系統G(t,τ)稱為系統的脈衝回響矩陣。
二、線性定常系統
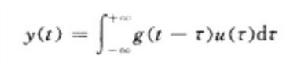 線性控制系統
線性控制系統單輸入—單輸出線性定常系統脈衝回響函式與具體的t、τ值無關,只與t-τ之差有關。於是輸入—輸出關係由式簡化為
同理,多輸入一多輸出線性定常系統的脈衝回響矩陣為G(t-τ),輸入一輸出關係由式簡化為
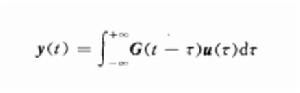 線性控制系統
線性控制系統狀態變數描述
狀態變數描述不僅能描述系統輸入與輸出之間的關係,而且在任意初始條件下,能揭示系統內部的行為,因此它是一種完全的描述,又稱內部描述。
一個物理系統可以用不同的方法來描述,例如用高階微分方程、傳遞函式、方框圖、結構圖等。
能完全表征系統時域行為的一組相互獨立的變數,稱為系統的狀態。組成這個變數組的變數x(t),x(t)......x(t)稱為狀態變數。
由狀態變數構成的列向量稱為系統的狀態向量,也簡稱狀態。以變數組的n個互相獨立的狀態變數x(t),x(t)......x(t)作為坐標軸而構造出來的n維空間叫做狀態空間。狀態空間是狀態向量取值的一個向量空間。系統某一時刻的狀態是空間中的一個點,狀態隨時間的變化過程,構成了狀態空間中的一條軌線。
描述系統輸入、輸出和狀態向量之間關係的方程稱為動態方程。對線性系統,其動態方程一般表示為
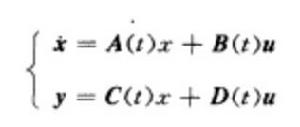 線性控制系統
線性控制系統其中第一式是描述系統狀態變化率的向量—矩陣微分方程,稱為狀態方程。第二式是描述系統輸出與系統狀態之間關係的方程,稱做輸出方程。u表示外部對系統的控制,稱為輸入向量。y是從外部量測系統運動狀態的量,稱為輸出向量。若x,u,y是維數分別為n,r,m的列向量,則矩陣A(t),B(t),C(t),D(t)分別具有的相應階數為n×n,n×r,m×n,m×r。它們的元素是時間t的連續函式。該式稱為線性時變動態方程。A(t)稱為系統矩陣,B(t)稱為輸入矩陣,C(t)為輸出矩陣,D(t)為前饋矩陣。矩陣D(t)表示從輸入u到輸出y的直接傳遞部分,為分析簡便,常令D(t)=n。狀態變數x(t),x(t)......x(t的個數n就是系統的維數。若方程中係數矩陣A,B,C,D不隨時間變化,則方程為線性定常動態方程。