簡介
線性無關集是線性空間中的一類子集。
設S是線性空間E的一個非空子集,如果S中任何有限個元都是線性無關的,則稱S為E的一個線性無關的集合。
線性空間
向量空間又稱線性空間,是線性代數的中心內容和基本概念之一。在解析幾何里引入向量概念後,使許多問題的處理變得更為簡潔和清晰,在此基礎上的進一步抽象化,形成了與域相聯繫的向量空間概念。譬如,實係數多項式的集合在定義適當的運算後構成向量空間,在代數上處理是方便的。單變元實函式的集合在定義適當的運算後,也構成向量空間,研究此類函式向量空間的數學分支稱為泛函分析。
向量空間它的理論和方法在科學技術的各個領域都有廣泛的套用。
線性無關
線性無關一般是指向量的線性獨立,指一組向量中任意一個向量都不能由其它幾個向量線性表示。
若有m+1個n維不全為零的向量
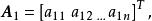 線性無關集
線性無關集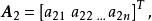 線性無關集
線性無關集 線性無關集
線性無關集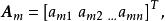 線性無關集
線性無關集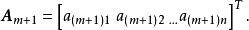 線性無關集
線性無關集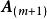 線性無關集
線性無關集如果其中第個向量可以寫成
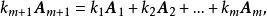 線性無關集
線性無關集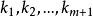 線性無關集
線性無關集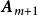 線性無關集
線性無關集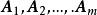 線性無關集
線性無關集這裡為常數,則稱這m+1個向量之間存在著線性關係;又稱這m+1個向量線性相關;或稱是的線性表出。當然,由上式可知若這m+1個向量是線性相關的,必可寫成
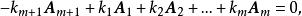 線性無關集
線性無關集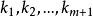 線性無關集
線性無關集這裡必不全為零。
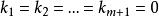 線性無關集
線性無關集顯然,若這m+1個向量不能夠寫成上面兩個式子的形式,或者換個說法只有當的情況下以上兩式才成立,則稱這m+1個向量是 線性無關的。
