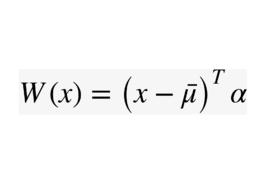定義
統計模式識別中用以對模式進行分類的一種最簡單的判別函式稱為線性判別函式。在特徵空間中，通過學習，不同的類別可以得到不同的判別函式，比較不同類別的判別函式值大小，就可以進行分類。統計模式識別方法把特徵空間劃分為決策區對模式進行分類。一個模式類同一個或幾個決策區相對應。每個決策區對應一個判別函式。對於特徵空間中的每個特徵向量 x ，可以計算相應於各個決策區的判別函式g(x)，i=1,2,…,c。
套用
人們已研究出多種求取決策邊界的算法。線性判別函式的決策邊界是一個超平面方程式，其中的係數可以從已知類別的學習樣本集求得。F.羅森布拉特的錯誤修正訓練程式是求取兩類線性可分分類器決策邊界的早期方法之一。在用線性判別函式不可能對所有學習樣本正確分類的情況下，可以規定一個準則函式（例如對學習樣本的錯分數最少）並用使準則函式達到最優的算法求取決策邊界。用線性判別函式的模式分類器也稱為線性分類器或線性機。這種分類器計算簡單，不要求估計特徵向量的類條件機率密度，是一種非參數分類方法。
當用貝葉斯決策理論進行分類器設計時，在一定的假設下也可以得到線性判別函式，這無論對於線性可分或線性不可分的情況都是適用的。在問題比較複雜的情況下可以用多段線性判別函式（見近鄰法分類、最小距離分類）或多項式判別函式對模式進行分類。一個二階的多項式判別函式可以表示為與它相應的決策邊界是一個超二次曲面。
距離判別
[discriminant by distance]
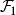線性判別函式
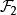線性判別函式
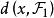線性判別函式
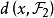線性判別函式所謂距離判別就是計算欲判類屬的樣本 x 到兩個總體和 的距離 和，按照如下準則來判別樣本的歸屬；
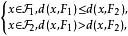線性判別函式
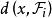線性判別函式其中距離 為馬哈拉諾比斯距離其定義為
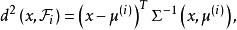線性判別函式
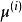線性判別函式
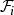線性判別函式
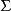線性判別函式 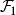線性判別函式 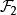線性判別函式為總體的均值向量， 是總體和的協方差距陣。容易算得
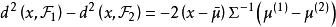線性判別函式
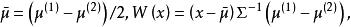線性判別函式令則判別準則可重新寫為
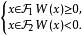線性判別函式
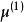線性判別函式
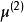線性判別函式 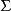線性判別函式
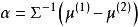線性判別函式當，，已知時，令，則有
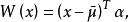線性判別函式
線性判別函式稱其為 線性判別函式， 稱為判別係數 (discriminant coefficient)。
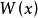線性判別函式
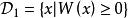線性判別函式
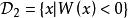線性判別函式
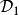線性判別函式
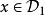線性判別函式
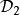線性判別函式
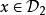線性判別函式
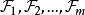線性判別函式 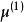線性判別函式
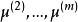線性判別函式
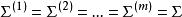線性判別函式這樣，利用線性判別函式 可以把空間劃分成兩部分：和。當樣本 x 落入 時，推斷；當樣本 x 落入時，推斷。當 m 個總體 時，其中各總體的均值分別為，，各總體的協方差距陣滿足，這時線性判別函式為
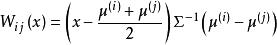線性判別函式
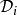線性判別函式
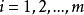線性判別函式
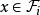線性判別函式其判別準則為：當 x 落入 內時，，判，其中
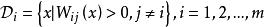線性判別函式。
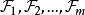線性判別函式
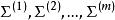線性判別函式當 m 個總體的協方差矩陣 不同時，令
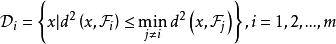線性判別函式 線性判別函式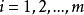 線性判別函式 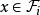線性判別函式則相應的判別準則為：當 x 落入內時， , 判斷。
