基本介紹
Fisher判別法是根據方差分析的思想建立起來的一種能較好區分各個總體的線性判別法，由Fisher在1936年提出。該判別方法對總體的分布不做任何要求。
Fisher判別法是一種投影方法，把高維空間的點向低維空間投影。在原來的坐標系下，可能很難把樣品分開，而投影后可能區別明顯。一般說，可以先投影到一維空間(直線)上，如果效果不理想，在投影到另一條直線上(從而構成二維空間)，依此類推。每個投影可以建立一個判別函式 。
下面給出Fisher判別法的詳細步驟。
兩個總體的Fisher判別函式
從兩個總體中抽取具有p個指標的樣品觀測數據，藉助於方差分析的思想構造一個線性判別函式：
Fisher判別法
Fisher判別法其中係數確定的原則是使兩組間的組間離差最大，而每個組的組內離差最小 。
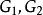Fisher判別法
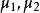Fisher判別法
Fisher判別法當建立了判別式以後，對一個新的樣品值，我們可以將他的p個指標值代人判別式中求出Y值，然後與判別臨界值比較，就可以將該樣品歸類。設有2個總體，其均值和協方差矩陣分別是和。可以證明，Fisher判別函式係數
Fisher判別法若總體均值與方差未知，可通過樣本進行估計。
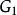Fisher判別法
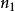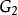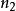Fisher判別法
Fisher判別法
Fisher判別法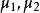
Fisher判別法
Fisher判別法 Fisher判別法
Fisher判別法
Fisher判別法設從第一個總體取得個樣本，從第二個總體取得個樣本，記兩組樣本均值分別為，樣本離差陣為。顯然，的無偏估計為。的估計有兩種方式。
第一種估計方式是分別估計
Fisher判別法判別函式為
Fisher判別法
Fisher判別法第二種估計方式是聯合估計
Fisher判別法於是判別函式
Fisher判別法
Fisher判別法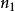 Fisher判別法 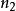Fisher判別法 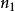Fisher判別法 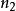Fisher判別法當時，兩種方法是等價的；當與相差不大時，兩種方法近似；當與相差很大時兩種方法相差較遠。目前採用較多的是第二種方法 。
多個總體的Fisher判別函式
Fisher判別法致力於尋找一個最能反映組和組之間差異的投影方向，即尋找使總體之間區別最大，而每個總體內部的離差平方和最小的線性判別函式 。
Fisher判別法
Fisher判別法
Fisher判別法設有k個總體，其均值和協方差矩陣分別是和。
Fisher判別法在的條件下，有
Fisher判別法
Fisher判別法令
Fisher判別法
Fisher判別法B相當於組間差，E相當於組內差。運用判別分析的思想，構造
Fisher判別法
Fisher判別法
Fisher判別法 Fisher判別法若求得極大值，即可得到判別函式。顯然，均為非負定矩陣。的極大值為方程
Fisher判別法的最大特徵根，而係數向量C為最大特徵根對應的特徵向量。
若總體均值與方差未知，可通過樣本進行估計。具體估計方法較為複雜，有興趣讀者可以參考有關書籍 。
判別規則
Fisher判別法如果我們得到判別函式，對於一個新的樣本Y，可以構造一個判別規則 ：
Fisher判別法
Fisher判別法，當
