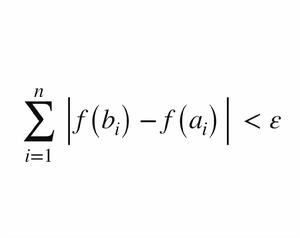簡介
絕對連續函式是一類極為重要的函式，設 f(x) 是 [a,b] 上的函式，若對任給 ε>0 ，存在 δ>0 ，使得對於在 [a,b] 上任意有限個互不相交的開區間 (a,b)，(a,b),...,(a,b)，當
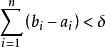絕對連續函式時，就有
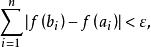絕對連續函式則 f(x) 稱為 [a,b] 上的一個絕對連續函式，令
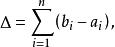絕對連續函式則 f(x) 在[a,b] 上絕對連續的充分必要條件為：當△→ 0 時，
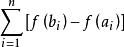絕對連續函式一致收斂於 0。
性質
絕對連續函式的名稱有維塔利 (Vitali,G.)提出，絕對連續函式的主要性質有：
1、若f(x) 與 g(x) 都是[a,b] 上的絕對連續函式，則
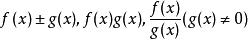絕對連續函式也是[a,b] 上的絕對連續函式.
2、若g(x) 是 [a,β] 上的絕對連續函式，a≤g(x)≤b，f(x) 在[a,b] 上滿足利普希茨條件，則 f[g(x)] 是[a,β] 上的絕對連續函式（但任意兩個絕對函式的複合函式未必絕對連續).
3、絕對連續函式一定是有界變差函式，但有界變差函式未必是絕對連續函式。
4、若f(x) 在 [a,b] 上絕對連續，且f‘(x)=0 a.e. 於 [a,b]，則f(x) 為一常數。
5、若f(x) 在 [a,b] 上絕對連續，且f‘(x)≥0 a.e. 於 [a,b]，則f(x) 為一單調增加函式。
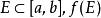絕對連續函式6、若f(x) 在[a,b] 上絕對連續，則 f(x) 具有性質 (N)，即對任何零集 仍為零集；性質(N) 對名稱由盧津 (JIyзин,H.H.）提出。
7、（巴拿赫-查列茨基定理）若 f(x) 是[a,b] 上的連續的有界變差函式，且具有性質 (N)，則 f(x) 是一絕對連續函式。
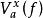絕對連續函式8、f(x) 在[a,b] 上絕對連續的充分必要條件為 是絕對連續函式。
9、絕對連續函式幾乎處處可微，是它的導函式的廣義原函式。
