性質
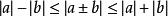絕對值不等式|a|表示數軸上的點a與原點的距離叫做數a的絕對值。
兩個重要性質：
1、|ab| = |a||b|
|a/b| = |a|/|b| （b≠0）
2、|a|<|b| 可逆推出 |b|>|a|
||a| - |b|| ≤ |a+b| ≤ |a|+|b|，若且唯若 ab≤0 時左邊等號成立，ab≥0 時右邊等號成立。
另外有：|a-b| ≤ |a|+|-b| = |a|+|-1|*|b| = |a|+|b|
| |a|-|b| | ≤ |a±b| ≤ |a|+|b|
幾何意義
1、當a，b同號時它們位於原點的同一邊，此時a與﹣b的距離等於它們到原點的距離之和。
2、當a，b異號時它們分別位於原點的兩邊，此時a與﹣b的距離小於它們到原點的距離之和。(|a-b|表示a-b與原點的距離，也表示a與b之間的距離)
相關公式
絕對值重要不等式推導過程 ：
我們知道|x|={x，(x>0);x，(x=0);-x，(x<0);
因此，有：
-|a|≤a≤|a| ......①
-|b|≤b≤|b| ......②
-|b|≤-b≤|b|......③
由①+②得：
-(|a|+|b|)≤a+b≤|a|+|b|
即 |a+b|≤|a|+|b| ......④
由①+③得：
-(|a|+|b|)≤a-b≤|a|+|b|
即 |a-b|≤|a|+|b| ......⑤
另：
|a|=|(a+b)-b|=|(a-b)+b|
|b|=|(b+a)-a|=|(b-a)+a|
由④知：
|a|=|(a+b)-b|≤|a+b|+|-b| => |a|-|b|≤|a+b|.......⑥
|b|=|(b+a)-a|≤|b+a|+|-a| => |a|-|b|≥-|a+b|.......⑦
|a|=|(a-b)+b|≤|a-b|+|b| => |a|-|b|≤|a-b|.......⑧
|b|=|(b-a)+a|≤|b-a|+|a| => |a|-|b|≥-|a-b|.......⑨
由⑥，⑦得：
| |a|-|b| |≤|a+b|......⑩
由⑧，⑨得：
| |a|-|b| |≤|a-b|......⑪
綜合④⑤⑩⑪得到有關 絕對值(absolute value)的重要不等式：|a|-|b|≤|a±b|≤|a|+|b|
要注意等號成立的條件（特別是求最值），即：
|a-b|=|a|+|b|→ab≤0
|a|-|b|=|a+b|→b(a+b)≤0
|a|-|b|=|a-b|→b(a-b)≥0
註：|a|-|b|=|a+b|→|a|=|a+b|+|b|→|（a+b）-b|=|a+b|+|b|→b(a+b)≤0
同理可得|a|-|b|=|a-b|→b(a-b)≥0
另 “→”指可雙向推出
解法
解決與絕對值有關的問題（如解絕對值不等式，解絕對值方程，研究含有絕對值符號的函式等等），其關鍵往往在於去掉絕對值符號。而去掉絕對值符號的基本方法有二。
以下，具體說說絕對值不等式的解法：
其一為平方，所謂平方，比如，|x|=3，可化為x^2=9，絕對值符號沒有了！
其二為討論，所謂討論，即x≥0時，|x|=x ；x<0時，|x|=-x，絕對值符號也沒有了！
說到討論，就是令絕對值中的式子等於0，分出x的段，然後根據每段討論得出的x值，取交集，綜上所述即可。
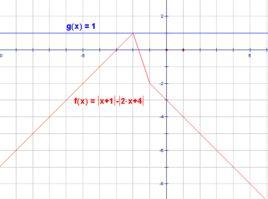
其三為數形結合法，即在數軸上將各點畫出，將數轉換為長度的概念求解。
